Системы линейных уравнений. Равносильные системы линейных уравнений. Решение системы линейных уравнений методом последовательного исключения переменных
Рассмотрим:
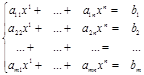 (1)
(1)
Составим матрицу при n-неизвестных.
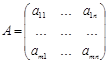
Эту матрицу называют матрицей системы(1)илиосновной матрицей. Если к ней добавить столбец, то вновь полученную матрицу называют расширенной.

Систему (1) удобно переписать в виде 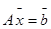 , где А-матрица столбца неизвестных
, где А-матрица столбца неизвестных 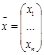
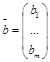 - столбец свободных членов
- столбец свободных членов
Система (1) называется однородной, если вектор b-нулевой, в противном случае - неоднородной.
Система (1) называется совместной, если она имеет хотя бы одно решение, т.е. переменным ( 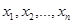 ) можно придать такие значения, которые будучи подставленными в (1) превращает уравнение в верное числовое равенство. Если система (1) решений не имеет, то ее называют несовместной.
) можно придать такие значения, которые будучи подставленными в (1) превращает уравнение в верное числовое равенство. Если система (1) решений не имеет, то ее называют несовместной.
Очевидно, что однородная система всегда совместна. 
Однородная система линейных уравнений.Очевидно, что если какое-либо уравнение системы заменить суммой этого уравнения и любого другого уравнения, умноженного на некоторое число, то вновь полученная система будет => первоначальной. Множество решений таких систем совпадает. Так же очевидно, что если два уравнения системы переставить местами, так же получим эквивалентную систему. Это значит, что с матрицей системы можно производить элементарные преобразования 1 и 2 видов.
Пусть 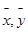 - решение однородной системы
- решение однородной системы 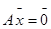 (2), покажем, что их линейная комбинация также будет решением этой системы
(2), покажем, что их линейная комбинация также будет решением этой системы 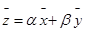 ;
; 
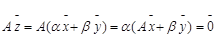 .
.
Это означает, что множество всех решений однородной системы V является подпространством пространства |  . Размерность этого подпространства = n-r, где r – ранг матрицы А.
. Размерность этого подпространства = n-r, где r – ранг матрицы А.
Пусть 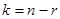 .
.
Базис линейного пространства V {f1, f2,…fk}называется фундаментальной системой решения (ФСР) системы (2). Зная ФСР можно записать любое решение однородной системы (2).
Алгоритм решения однородной системы:
1.Выписываем матрицу системы.
2.Приводим матрицу к ступенчатому виду.
3.Переменные, соответствующие угловым коэффициентам в ступенчатой матрице, назовем зависимыми, а оставшиеся – независимыми. Затем выразим зависимые переменные через независимые. Кол-во зависимых = r(рангу матрицы), количество независимых (свободных) = k.
4.Векторы ФСР можно получить так: одной из свободных переменных придаем 1, а остальным – 0, и вычисляем значение зависимых переменных. Получаем 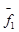 , придавая значение 1 другой переменной, получим другой вектор
, придавая значение 1 другой переменной, получим другой вектор 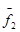 и т.д., пока не получим ФСР.
и т.д., пока не получим ФСР.
5.Общее решение системы f будет иметь вид 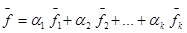 , где α1,α2,…αk - произвольные числа.
, где α1,α2,…αk - произвольные числа.
Неоднородные системы линейных ур-й. Метод Гаусса.
Дана система:
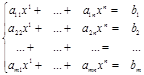 (1)
(1)
В системе (1) хотя бы одно из чисел 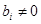 . Обозначим
. Обозначим 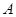 - матрицу этой системы,
- матрицу этой системы, 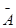 - матрицу расширенную. Систему (1) можно переписать в векторном виде
- матрицу расширенную. Систему (1) можно переписать в векторном виде
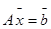 (1), где
(1), где 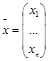 ,
, 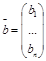 .
.
Наряду с системой (1) будем рассматривать однородную систему (2), которую назовем соответствующей системе (1).
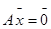 (2)
(2)
Неоднородная система может быть несовместной, т.е. не иметь решений.
Теорема (Кронекера-Капелли)
Неоднородная система (1) совместна тогда и только тогда, когда ранг ее основной матрицы=рангу расширенной ( 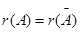 ).
).
Пусть х – решение системы (1), а у – решение системы (2). Тогда 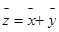 -решение систем
-решение систем 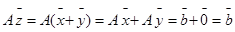 , т.о.
, т.о. 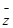 - является решением системы (1)
- является решением системы (1)
Т.о. если к частному решению системы (1) прибавить какое-нибудь решение, соответствующей однородной системы (2), то снова получим решение системы (1).
Т.о. можно получить любое решение системы (1).
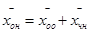 (3), где
(3), где 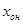 - общая неоднородная система;
- общая неоднородная система; 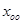 - общая однородная;
- общая однородная; 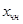 - частная неоднородная
- частная неоднородная
Поэтому для отыскания решения системы (1) необходимо найти какое-нибудь частное решение системы (1), найти все решения соответствующее неоднородной системы и воспользоваться формулой (3).
Метод Гаусса- классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
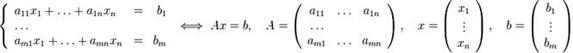
Матрица A наз. основнойматрицей системы, b - столбцом свободных членов.
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа:
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из кот. выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Пример: Решить систему уравнений
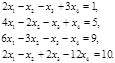
Решение. Будем решать методом Гаусса. Выпишем расширенную матрицу системы и преобразуем её, вычитая первую строку, умноженную на 2, 3 и 1 соответственно из 2-ой, 3-ей и 4-ой строк:

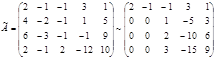
Далее вторую строку, умноженную на 2 и 3, вычтем соответственно из третей и четвёртой строк:

Последняя матрица эквивалентна следующей ступенчатой системе: 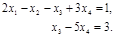
Полученная упрощённая система представляет собой систему из двух уравнений для четырёх неизвестных. Следовательно, два из неизвестных можно выбрать за главные, а два - за свободные, через кот. будут выражены главные. В качестве главных неизвестных можно выбрать любую пару, если определитель, составленный из коэффициентов, стоящих перед ними, отличен от нуля (базисный
минор). В данной задаче в качестве главных неизвестных можно выбрать 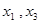 .
.
Действительно, определитель, составленный из их коэффициентов, отличен от нуля: 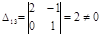 .
.
Теперь из второго уравнения выразим 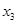 через
через 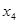 . Затем подставим его в первое уравнение и найдём
. Затем подставим его в первое уравнение и найдём  через
через 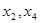 . В итоге получим:
. В итоге получим: 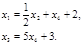
Переменные 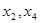 принимают произвольные значения. Положив
принимают произвольные значения. Положив 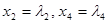 , общее решение системы можно записать в виде:
, общее решение системы можно записать в виде:
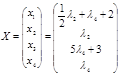
Дата добавления: 2015-07-30; просмотров: 4081;
