Поле комплексных чисел. Геометрическое представление комплексных чисел и операции над ними. Тригонометрическая форма комплексного числа
Комплексным числом zназ. выражение 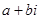 , где а и в – вещественные числа, i – мнимая единица или специальный знак.
, где а и в – вещественные числа, i – мнимая единица или специальный знак.
При этом выполняются соглашения:
1) с выражением a+bi можно производить арифметические операции по правилам, которые приняты для буквенных выражений в алгебре;
2) i2=-1;
3) a+0i=a;
4) 0+bi=bi
5) равенство a+bi=c+di, где a, b, c, d – действительные числа, имеет место тогда и только тогда, когда a=c и b=d.
Число 0+bi=bi называется мнимым или чисто мнимым.
Любое действительное число а есть частный случай комплексного числа, ведь его можно записать в виде a=a+ 0i. В частности, 0=0+0i, но тогда ели a+bi=0, то a+bi=0+0i, следовательно, a=b=0.
Т.о., комплексное число a+bi=0 тогда и только тогда, когда a=0 и b=0.
Из соглашений следуют законы преобразования комплексных чисел:
(a+bi)+(c+di)=(a+c)+(b+d)i;
(a+bi)-(c+di)=(a-c)+(b-d)i;
(a+bi)+(c+di)=ac+bci+adi-bd=(ac-bd)+(bc+ad)i;
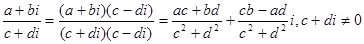
Мы видим, что сумма, разность, произведение и частное (где делитель не равен нулю) комплексных чисел, в свою очередь комплексное число.
Число а наз. вещественной частью комплексного числа z (обозначается 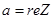 ), в – мнимая часть комплексного числа z (обозначается
), в – мнимая часть комплексного числа z (обозначается 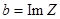 ).
).
Комплексное число z с нулевой вещественной частью наз. чисто мнимым, с нулевой мнимой – чисто вещественным.
Два комплексных числа наз.равными,если у них совпадают и вещественная и мнимая части.
Два комплексных числа наз. сопряженными, если у них веществ. части совпадают, а мнимые отличаются знаками. 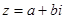 , то сопряженное к нему
, то сопряженное к нему 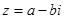 .
.
Сумма сопряженных чисел есть число веществ, а разность чисто мнимое число. На множестве комплексных чисел естественным образом определены операции умножения и сложения чисел. Именно, если 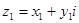 и
и 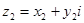 - два комплексных числа, то сумма:
- два комплексных числа, то сумма: 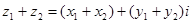 ; произведение:
; произведение: 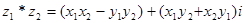 .
.
Определим теперь операции вычитания и деления.
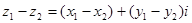
Заметим, что произведение двух комплексных чисел есть число веществ.
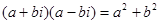 (т.к. i=-1). Это число наз. квадратом модуля числа
(т.к. i=-1). Это число наз. квадратом модуля числа 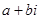 . Т.о., если число
. Т.о., если число 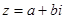 , то его модуль
, то его модуль 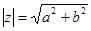 есть вещественное число.
есть вещественное число.
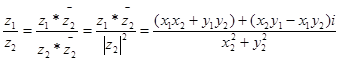 (деление на 0 запрещено)
(деление на 0 запрещено)
В отличие от вещественных чисел для комплексных чисел не вводится понятие «больше», «меньше».
Геометрическое представление комплексных чисел.Действительные числа изображаются точками на числовой прямой:

Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (рис.). Эта система координат называется комплексной плоскостью.
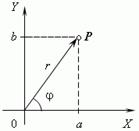
Модулемкомплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:
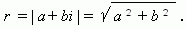
Сопряжённые комплексные числа имеют одинаковый модуль. __
Аргументкомплексного числа - это угол 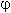 между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan
между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan 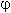 = b / a .
= b / a .
Тригонометрическая формакомплексного числа. Наряду с записью комплексного числа в алгебраической форме также употребляется и другая, называемая тригонометрической.
Пусть комплексное число z=a+bi изображается вектором ОА с координатами (a,b). Обозначим длину вектора ОА буковой r: r=|ОА|, а угол, который он образует с положительным направлением оси Ох – через угол φ.
Воспользовавшись определениями функций sinφ=b/r, cosφ=a/r, комплексное число z=a+bi можно записать в виде z=r(cosφ+i*sinφ), где 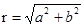 , а угол φ определяется из условий
, а угол φ определяется из условий 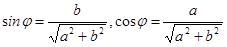
Тригонометрической формой комплексного числа z называется его представление в виде z=r(cosφ+i*sinφ), где r и φ – действительные числа и r≥0.
Действительно число r называется модулем комплексного числа и обозначается |z|, а угол φ – аргументом комплексного числа z. Аргумент φ комплексного числа z обозначается Arg z.
Операции с комплексными числами, представленными в тригонометрической форме:
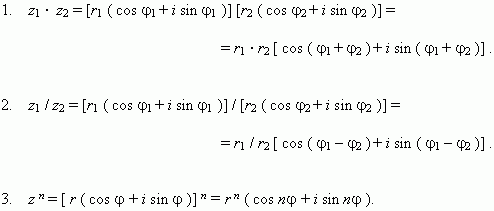
Это знаменитая формула Муавра.
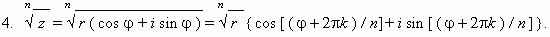
8.Векторное пространство. Примеры и простейшие свойства векторных пространств. Линейная зависимость и независимость системы векторов. Базис и ранг конечной системы векторов
Векторное пространство - математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трёхмерного пространства.
Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа. В применении к любым векторам х, у, z и любым числам α, β эти правила удовлетворяют следующим условиям:
1) х+у=у+х (коммутативность сложения);
2)(х+у)+z=x+(y+z) (ассоциативность сложения);
3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x+0=x: для любого вектора x;
4) для любого вектора х существует противоположный ему вектор у такой, что х+у =0,
5) 1 · х=х, где 1 – единица поля
6) α(βx)=(αβ)х (ассоциативность умножения), где произведение αβ есть произведение скаляров
7) (α+β)х=αх+βх (распределительное свойство относительно числового множителя);
8) α(х+у)=αх+αу(распределительное свойство относительно векторного множителя).
Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям 1-8.
Примерами таких пространств могут служить множество действительных чисел, множество векторов на плоскости и в пространстве, матрицы и т.д.
Теорема “Простейшие свойства векторных пространств”
1. В векторном пространстве существует единственный нулевой вектор.
2. В векторном пространстве любой вектор имеет единственный противоположный ему.
3. 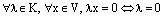 или
или 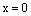 .
.
4. 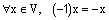 .
.
Док-во
Пусть 0 – нулевой вектор векторного пространства V. Тогда 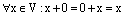 . Пусть
. Пусть 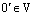 – еще один нулевой вектор. Тогда
– еще один нулевой вектор. Тогда 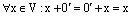 . Возьмем в первом случае
. Возьмем в первом случае 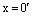 , а во втором –
, а во втором – 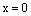 . Тогда
. Тогда 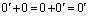 и
и 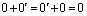 , откуда следует, что
, откуда следует, что 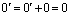 , ч.т.д.
, ч.т.д.
Сначала мы докажем, что произведение нулевого скаляра на любой вектор равен нулевому вектору.
Пусть 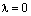 . Тогда, применяя аксиомы векторного пространства, получаем:
. Тогда, применяя аксиомы векторного пространства, получаем:
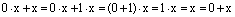
Относительно сложения векторное пространство является абелевой группой, а в любой группе справедлив закон сокращения. Применяя закон сокращения, из последнего равенства следует 0*х=0
Теперь докажем утверждение 4). Пусть 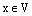 – произвольный вектор. Тогда
– произвольный вектор. Тогда
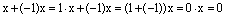
Отсюда сразу же следует, что вектор (-1)х является противоположным вектору х.
Пусть теперь х=0. Тогда, применяя аксиомы векторного пространства, 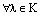 и
и  получаем:
получаем:
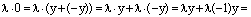
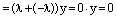
Пусть 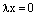 и допустим, что
и допустим, что 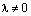 . Так как
. Так как 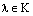 , где К – поле, то существует
, где К – поле, то существует 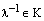 . Умножим равенство
. Умножим равенство 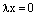 слева на
слева на 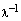 :
: 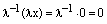 , откуда следует
, откуда следует 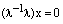 или 1*х=0 или х=0
или 1*х=0 или х=0
Линейная зависимость и независимость системы векторов. Набор векторов  называется системой векторов.
называется системой векторов.
Система из 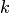 векторов
векторов  называется линейно-зависимой, если существуют такие числа
называется линейно-зависимой, если существуют такие числа 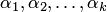 , не все равные нулю одновременно, что
, не все равные нулю одновременно, что 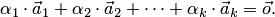 (1)
(1)
Система из k векторов  называется линейно-независимой, если равенство (1) возможно только при
называется линейно-независимой, если равенство (1) возможно только при 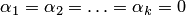 , т.е. когда линейная комбинация в левой части равенства (1) тривиальная.
, т.е. когда линейная комбинация в левой части равенства (1) тривиальная.
Замечания:
1. Один вектор 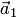 тоже образует систему: при
тоже образует систему: при 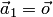 линейно-зависимую, а при
линейно-зависимую, а при 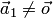 линейно независимую.
линейно независимую.
2. Любая часть системы векторов называется подсистемой.
Свойства линейно зависимых и линейно независимых векторов:
1. Если в систему векторов входит нулевой вектор, то она линейно-зависима.
2. Если в системе векторов имеется два равных вектора, то она линейно-зависима.
3. Если в системе векторов имеется два пропорциональных вектора 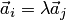 , то она линейно-зависима.
, то она линейно-зависима.
4. Система из k>1 векторов линейно-зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.
5. Любые векторы, входящие в линейно-независимую систему, образуют линейно-независимую подсистему.
6. Система векторов, содержащая линейно-зависимую подсистему, линейно-зависима.
7. Если система векторов  линейно-независима, а после присоединения к ней вектора
линейно-независима, а после присоединения к ней вектора 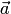 оказывается линейно-зависимой, то вектор
оказывается линейно-зависимой, то вектор 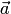 можно разложить по векторам
можно разложить по векторам  , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.
, и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.
Докажем, например, последнее свойство. Так как система векторов 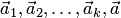 — линейно зависима, то существуют числа
— линейно зависима, то существуют числа 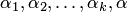 , не все равные 0, что . В этом равенстве
, не все равные 0, что . В этом равенстве 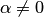 . В самом деле, если
. В самом деле, если  , то . Значит, нетривиальная линейная комбинация векторов
, то . Значит, нетривиальная линейная комбинация векторов  равна нулевому вектору, что противоречит линейной независимости системы
равна нулевому вектору, что противоречит линейной независимости системы  . Следовательно,
. Следовательно, 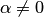 и тогда , т.е. вектор
и тогда , т.е. вектор 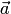 есть линейная комбинация векторов
есть линейная комбинация векторов  . Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения
. Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения 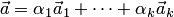 и
и 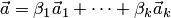 , причем не все коэффициенты разложений соответственно равны между собой (например,
, причем не все коэффициенты разложений соответственно равны между собой (например,  ).
).
Тогда из равенства 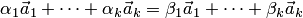 получаем
получаем 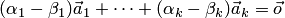 .
.
Следовательно, линейная комбинация векторов  равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере
равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере 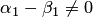 ), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов
), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов  . Полученное противоречие подтверждает единственность разложения.
. Полученное противоречие подтверждает единственность разложения.
Ранг и базис системы векторов. Рангом системы векторов называется максимальное число линейно-независимых векторов системы. 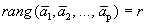
Базисом системы векторов называется максимальная линейно независимая подсистема данной системы векторов.
Теорема. Любой вектор системы можно представить в виде линейной комбинации векторов базиса системы. (Всякий вектор системы можно разложить по векторам базиса.) Коэффициенты разложения определяются для данного вектора и данного базиса однозначно.
Док-во:
Пусть система 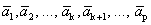 имеет базис
имеет базис 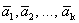 .
.
1 случай. Вектор 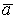 - из базиса. Следовательно, он равен одному из векторов базиса, допустим
- из базиса. Следовательно, он равен одному из векторов базиса, допустим 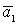 . Тогда
. Тогда 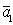 =
= 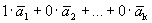 .
.
2 случай. Вектор 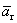 - не из базиса. Тогда r>k.
- не из базиса. Тогда r>k.
Рассмотрим систему векторов 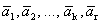 . Данная система является линейно зависимой, так как
. Данная система является линейно зависимой, так как 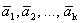 - базис, т.е. максимальная линейно независимая подсистема. Следовательно, найдутся числа с1, с2, …, сk, с, не все равные нулю, такие, что
- базис, т.е. максимальная линейно независимая подсистема. Следовательно, найдутся числа с1, с2, …, сk, с, не все равные нулю, такие, что
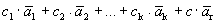 =
= 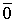 .
.
Очевидно, что 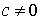 (если с=0, то базис системы является линейно зависимым).
(если с=0, то базис системы является линейно зависимым).
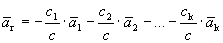 .
.
Докажем, что разложение вектора по базису единственно. Предположим противное: имеется два разложения вектора по базису.
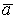 =
= 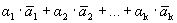 ,
,
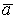 =
= 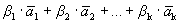 .
.
Вычитая эти равенства, получим 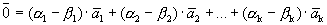
Учитывая линейную независимость векторов базиса, получим 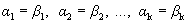
Следовательно, разложение вектора по базису единственно.
Количество векторов в любом базисе системы одинаково и равно рангу системы векторов.
Дата добавления: 2015-07-30; просмотров: 6013;
