Степенная функция с натуральным, целым и рациональным показателем. Определение степени с действительным показателем

Пусть n – натуральное число. Функция y=xⁿ, -∞<x<+∞, называется степенной функцией с натуральным показателем n.

Она определена на действительной оси и непрерывна. Непрерывность доказывается по индукции. В самом деле, при n=1 это функция y=x, очевидно непрерывная. Если допустить, что функция y=x^k-1 непрерывна, то y=x^k=x*x^k-1 непрерывна как произведение двух непрерывных функций: y=x и y=x^k-1. Т.о., на основании принципа индукции, каково бы ни было натуральное число n, функция y=xⁿ непрерывна на интервале (-∞; +∞).

Рассмотрим степенную функцию только для неотрицательных значений x, т.е. только на полуинтервале [0;+∞): y=xⁿ, 0≤x<+∞. Непрерывность этой функции мы установили, окажем, что она возрастает, т.е. если 0≤x₁<x₂, то x₁ⁿ<x₂ⁿ.

При n=1 это свойство тривиально.

Допустим, что оно верно для произвольного натурального k, т.е. если 0≤x₁<x₂, то x₁^k<x₂^k, тогда x₂^k+1-x₁^k+1= x₂^k(x₂-x₁)+x1(x₂^k -x₁^k). Первое слагаемое в правой части равенства положительно, а второе неотрицательно, поэтому правая часть равенства положительна, а следовательно, и x₂^k+1-x₁^k+1>0. Тогда на основании принципа индукции доказано, что если 0≤x₁<x₂, то x₁ⁿ<x₂ⁿ при любом натуральном n.

На рисунке изображен график функции y=xⁿ на полуинтервале [0;+∞). Из графика видно, что, когда x непрерывно возрастает, пробегая все точки полуинтервала [0;+∞), y тоже непрерывно возрастает, пробегая интервал [0;+∞)один раз. Т.о., областью определения функции является полуинтервал [0;+∞), областью значений y является полуинтервал [0;+∞).

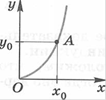
Корнем n-й степенииз числа y называется число x, такое, что его n-я степень равна y(y=xⁿ). Корень n-й степени обозначают: . Неотрицательный корень n-й степени из неотрицательного числа y называется арифметическим корнем n-й степени.

Покажем, что арифметический корень n-й степени из неотрицательного числа всегда существует и притом единственный. Рассмотрим функцию y=xⁿ для x€[0;+∞). Зададим произвольное неотрицательно число y₀, отметим на оси ординат точку (0, y₀) и проведем через нее прямую, параллельную оси Ox. Она пересечет график в одной точке (точке А) абсцисса которой x₀ и есть арифметический корень n-й степени из данного числа y₀.

Рассмотри функцию y=xⁿ, -∞<x<+∞, n=2m, m=1,2,…

В силу равенства y(-x)=(-x)^2m=((-x)²)^m=x^2m=y(x) функция четная и ее график симметричен относительно оси Oy. На рисунке изображен схематичный график функции. Он расположен выше оси Ox и только в одной точке, – в начале координат – он касается оси Ox. Зададим число y₀>0, отметим на оси ординат точку (0,y₀) и проведем через нее прямую, параллельную оси Ox, до пересечения с графиком. Как видим, прямая пересекает график в двух точках А и В, симметричных относительно оси Oy. Абсциссы этих точек x₀ и –x₀ обладают тем свойством, что их n-я степень равна числу y₀. Абсциссы всех остальных точек этим свойством не обладают. Это показывает, что числа x₀ и –x₀ являются корнями n-й степени из числа y₀ и других корней степени n из y₀ нет.

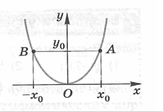
Число x₀ – положительный корень n-й степени из y₀: , это арифметический корень. Другой корень равен , это не арифметический корень. Оба могут быть записаны так:. Подчеркнем, что случай y=0 охватывается формулой, дающей при этом единственный корень .

При любом натуральном n и x≥0 выполняется равенство . Пусть x – число любого знака. Т.к. , то. Но если n=2m четное, то , поэтому для любого x при четном n справедлива формула .

Рассмотри степенную функцию y=xⁿ, -∞<x<+∞, n=2k+1, k=0,1,2,…

Она определена на всей действительной оси и нечетная: y(-x)=(-x)^2k+1=(-x)*(-x)^2k=-x* x^2k=- x^2k+1=-y(x). Поэтому ее график симметричен относительно начала координат. Из графика следует, что функция непрерывна, возрастает на всей действительной оси и обладает свойством: .

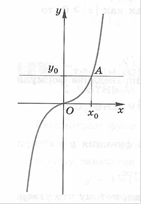
Областью изменения функции является интервал (-∞; +∞). Зададим произвольное число y₀ и отметим на оси ординат точку (0, y₀). Проведем через нее прямую, параллельную оси Ox. Она пересечет график в единственной точке А, абсцисса x₀, которой и есть единственный корень n-й степени из y₀, причем , при y₀≥0 и при y₀<0, т.е. определена функция:

Т.о., при нечетном n формула определена для любых y и для каждого y€(-∞;+∞) задает x – единственный корень n-й степени из y. Этот корень является арифметическим только для неотрицательных y.

Случаи четного и нечетного n различаются следующим:

1)при y>0 в случае нечетного n существует единственный корень n-й степени из y – это , в случае четного n – два корня ;

2) при y<0 в случае нечетного n существует единственный корень , а при четном n арифметических корней нет.

Выражение aⁿ (степень с целым показателем) будет определено во всех случаях, за исключением случая, когда a = 0 и при этом n меньше либо равно нулю.

Основные свойства степеней с целым показателем:

a^m *aⁿ = a^(m+n);

a^m : aⁿ = a^(m-n) ( при a не равном нулю);

(a^m)ⁿ = a^(m*n);

(a*b)ⁿ = aⁿ *bⁿ;

(a/b)ⁿ = (aⁿ)/(bⁿ) (при b не равном нулю);

a¹ = a;

a⁰ = 1 ( при a не равном нулю);

Эти свойства будут справедливы для любых чисел a, b и любых целых чисел m и n.

Для любых рациональных чисел p, q и любых a>0 и b>0 верны следующие равенства:

1. (a^p)*(a^q) = a^(p+q);

2. (a^p):(b^q) = a^(p-q);

3. (a^p)^q = a^(p*q);

4. (a*b)^p = (a^p)*(b^p);

5. (a/b)^p = (a^p)/(b^p).

Док-во первого равенства (a^p)*(a^q) = a^{(p + q)}.

Пусть p = m/n, a q = k/l, где n, l - некоторые натуральные числа, а m, k – некоторые целые числа. Тогда нужно доказать, что:

(a^(m/n))*(a^(k/l)) = a^{((m/n) + (k/l))}.

Сначала приведем дроби m/n k/l к общему знаменателю. Получим дроби (m*l)/(n*l) и (k*n)/(n*l). Перепишем левую часть равенства с помощью этих обозначений и получим:

(a^(m/n))*(a^(k/l)) = (a^{((m*l)/(n*l))})*(a^{((k*n)/(n*l))}).

Далее получим:

(a^(m/n))*(a^(k/l)) = (a^{((m*l)/(n*l))})*(a^{((k*n)/(n*l))}) = (n*l)√(a^(m*l))*(n*l)√(a^(k*n)) = (n*l)√( (a^(m*l))*(a^(k*n))) = (n*l)√(a^(m*l+k*n)) = a^{((m*l+k*n)/(n*l))} = a^{((m/n)+(k/l))}.

То есть получили, что (a^(m/n))*(a^(k/l)) = a^{((m/n)+(k/l))}, что и требовалось доказать.