I. Определение исходного опорного решения.

Используем метод двойного преимущества. Идея этого метода состоит в выборе клеток в матрице стоимости с минимальными значениями стоимостей и в последующем назначением перевозок по маршрутам, образованными выбранными клетками.

Первоначально выбираются клетки с минимальной стоимостью каждой строке, потом в каждом столбце. Найденные клетки помечаются точками.

В результате все клетки матрицы стоимости будут разделены на 3 категории:

1) клетки с двумя точками (оценками),

2) клетки с одной оценкой,

3) клетки без оценок.

Основной поток перевозок осуществляется по маршрутам, образованным клетками матрицы с двумя оценками, потом используются маршруты через клетки с одной оценкой.

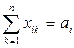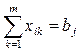Если с помощью этих маршрутов не удается выполнить условие и , то назначаются маршруты через клетки без оценок.

II. После выбора опорного плана необходимо проверить его на
оптимальность.

Перед проверкой матрицы стоимости следует добиваться выполнения условий, которым должен соответствовать оптимальный план:

1.Оптимальный план состоит из (m+n-1) базисных клеток. Если число базисных клеток меньше, чем (m+n-1), необходимо ввести фиктивный объем перевозок .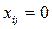

2.В оптимальном плане не может быть циклов.

Циклом называется ломаная линия, вершины которой расположены в клетках матрицы стоимости, которая начинается и заканчивается одним и тем же элементом. При этом только любые два соседних элемента расположены в одной строке (столбце).

Для определения оптимального плана транспортной задачи используем
метод потенциалов.

Для этого каждому пункту отправления сопоставим некоторую величину 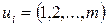, которую назовем потенциалом пункта отправления A_i и каждому пункту назначения B_j величину 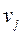- потенциал пункта B_j.

Тогда условия оптимальности принятого плана можно записать в виде:
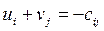, для всех 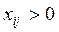, (8)

т.е. для клеток матрицы, которые составляют маршрут перевозки,
и 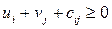(9)

если клетка ij матрицы не определяет маршрут перевозки.

Для решения системы (8) значение одного из неизвестных зададим произвольно одним из способов:

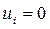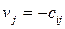1. Если , то (10)

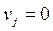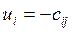2. Если , то (11)

Затем вычисляются оставшиеся неизвестные элементы.

После этого необходимо эквивалентно преобразовать матрицу стоимости, каждый элемент которой теперь будет представлять собой алгебраическую сумму одноименного элемента предыдущей матрицы и соответствующих элементов 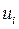и .

Таким образом, план перевозок считается оптимальным, если в матрице стоимости после преобразования элементов в клетках, которые обозначают маршрут перевозки (базисные клетки), значения равны нулю (8), а в других клетках большие или равны нулю(9).

Если матрица стоимости содержит отрицательные элементы, то необходимо скорректировать план перевозок.

Для этого:

1. Выбирают максимальный по модулю отрицательный элемент матрицы.

2. Из клетки этого элемента строят цикл (по часовой стрелке) по другим выделенным элементам матрицы с последовательной нумерацией вершин цикла римскими цифрами.

3.Найденный цикл переносят на транспортную таблицу и из всех четных вершин цикла, выбирают вершину с минимальным объемом перевозок.

4. Этот объем отнимается ото всех объемов перевозок, которые находятся в четных вершинах цикла, и прибавляется к объему перевозок в нечетных вершинах цикла. Такое перераспределение приводит к новому плану, который в свою очередь надо проверить на оптимальность.

На каждом этапе преобразования транспортной таблицы, необходимо вычислить общие затраты F. При этом величина целевой функции F уменьшается от плана к плану на размер равный произведению отрицательного элемента матрицы и минимального объема перевозок в вершинах цикла.