Логарифмическая и обратные тригонометрические функции
Функцию вида y = loga(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а. Обозначения логарифма loga(b) - данная запись означает логарифм b по основанию а.
Основные свойства логарифмической функции:
1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.
2. Областью значения логарифмической функции будет являться все множество вещественных чисел.
3. Если основание логарифмической функции a>1, то на всей области определения функции возрастает. Если для основания логарифмической функции выполняется следующее неравенство 0<a
4. График логарифмической функции всегда проходит через точку (1;0).
5. Возрастающая логарифмическая функция, будет положительной при x>1, и отрицательной при 0<х<1.
6. Убывающая логарифмическая функция, будет отрицательной при х>1, и положительной при 0<x<1:
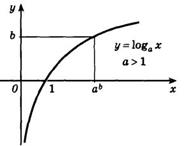
На следующем рисунке представлен график убывающей логарифмической функции - (0<a<1):
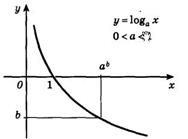
7. Функция не является четной или нечетной.
8. Функция не имеет точек максимума и минимума.
Обратные тригонометрические функции, также круговые функции или аркфункции — математические функции, являющиеся обратными к тригонометрическим функциям.
Основные обратные тригонометрические функции:
1.Арксинус – arcsin
Арксинусом числа a , где , называется такой угол x, для которого sin x=a, где . Функция y=arcsin x является строго возрастающей.
Учтем, что sin(arcsin x)=x, ; arcsin(sin x)=x,
Свойства функции arcsin x:
1) arcsin(-x)=-arcsin x;
2) arcsin x=
3) arcsin x=
2.Арккосинус – arccos
Арккосинусом числа a называется такой угол x , для которого cos x=a , где 0≤x≤π, . Функция y=arccos x является строго убывающей.
Учтем, что: cos(arccos x)=x, ; arccos(cos x)=x,0≤x≤π
Свойства функции arcos x:
1) arccos(-x)=π-arccos x;
2) arccos x=
3) arccos x=
3. Арктангенс – arctg
Арктангенсом числа a называется такой угол x , для которого tg x=a, .
Функция y=arctg x непрерывна и ограничена на всей числовой прямой и является строго возрастающей.
Свойства функции arctg x:
1)
2)
4. Арккотангенс – arcctg
Арккотангенсом числа a называется такой угол x , для которого ctg x=a, 0<x<π.
Функция y=arcctg непрерывна и ограничена на всей числовой прямой и является строго убывающей.
Свойства функции arcctg:
1)
2) arcctg x=
Существуют два основных соотношения между обратными функциями:
arcsin x+arccos x=π/2;
arctg x+arcctg x=π/2;
Функции arcsin x и arccos x определены на отрезке [-1, 1], а arctg x и arcctg x - на всей числовой прямой.
Их графики изображены на рисунках:
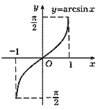
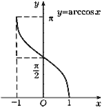
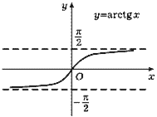
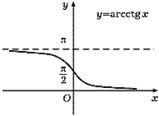
Дата добавления: 2015-07-30; просмотров: 2973;
