Понятие о квадрируемой фигуре на плоскости и ее площади. Вычисление площади с помощью интеграла
Введем понятие площади плоской фигуры Q - части плоскости, ограниченной простой замкнутой кривой L (разделяет плоскость на две части - внутреннюю и внешнюю). При этом кривую L будем называть границей фигуры Q.
Будем говорить, что многоугольник вписан в фигуру Q, если каждая точка этого многоугольника принадлежит фигуре Q или ее границе. Если все точки плоской фигуры и ее границы принадлежат некоторому многоугольнику, то будем говорить, что указанный многоугольник описан вокруг фигуры Q.
Ясно, что площадь любого вписанного в фигуру Q многоугольника не больше площади любого описанного вокруг фигуры Q многоугольника.
Пусть {Si} - числовое множество площадей вписанных в плоскую фигуру Q многоугольников, а {Sd} - числовое множество площадей описанных вокруг фигуры Q многоугольников. Очевидно, множество {Si} ограничено сверху (площадью любого описанного вокруг фигуры Q многоугольника), а множество {Sd} ограничено снизу (например, числом нуль). Обозначим через точную верхнюю грань множества {Si}, а через - точную нижнюю грань множества {Sd}. Числа и называются соответственно нижней площадью и верхней площадью фигуры Q. Отметим, что нижняя площадь фигуры Q не больше верхней площади этой фигуры, т. е. . В самом деле, предположим, что верно противоположное неравенство . Тогда, полагая и учитывая определение точных граней, найдем такой вписанный в фигуру Q многоугольник, площадь Si которого будет больше числа и такой описанный вокруг фигуры Q многоугольник, площадь Sd которого меньше числа . Сопоставляя полученные два неравенства, найдем, что Sd < Si, чего не может быть, так как площадь Sd любого описанного многоугольника не меньше площади Si любого вписанного многоугольника.
Плоская фигура Q называется квадрируемой, если верхняя площадь этой фигуры совпадает с ее нижней площадью . При этом число называется площадью фигуры Q.
Теорема 1: Для того чтобы плоская фигура Q была квадрируемой, необходимо и достаточно, чтобы для любого положительного числа ε можно было указать такой описанный вокруг фигуры Q многоугольник и такой вписанный в фигуру Q многоугольник, разность Sd - Si площадей которых была бы меньше ε, Sd - Si < ε.
Док-во:
1) Необходимость. Пусть фигура Q квадрируема, т. е. . Так как и - точные верхняя и нижняя грани множеств {Si} и {Sd}, то для любого числа ε > 0 можно указать такой вписанный в фигуру Q многоугольник, площадь Si которого отличается от меньше чем на ε/2, т. е. P-Si < ε/2. Для этого же ε > 0 можно указать такой описанный многоугольник, площадь Sd которого отличается от меньше чем на ε/2, т. е. Sd - P < ε/2. Складывая полученные неравенства, найдем, что Sd - Si < ε.
2) Достаточность. Пусть Sd и Si - площади многоугольников, для которых Sd - Si < ε. Так как 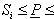
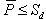 , то . В силу произвольности ε отсюда вытекает, что . Таким образом, фигура квадрируема. Теорема доказана.
, то . В силу произвольности ε отсюда вытекает, что . Таким образом, фигура квадрируема. Теорема доказана.
Будем говорить, что граница плоской фигуры Q имеет площадь, равную нулю, если для любого положительного ε > 0 можно указать такой описанный вокруг фигуры Q многоугольник и такой вписанный в фигуру Q многоугольник, разность Sd - Si площадей которых меньше ε. Очевидно, теорему 1 можно также сформулировать следующим образом:для того чтобы плоская фигура Q была квадрируемой, необходимо и достаточно, чтобы ее граница имела площадь, равную нулю.
Площадь криволинейной трапеции.Криволинейной трапецией называется фигура, ограниченная графиком заданной на сегменте [a, b] непрерывной и неотрицательной фукнции f(x), ординатами, проведенными в точках a и b, и отрезком оси Ox между точками a и b.
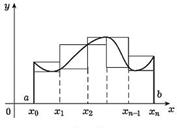
Докажем следующее утверждение: Криволинейная трапеция представляет собой квадрируемую фигуру, площадь P которой может быть вычислена по формуле:
Док-во: Так как непрерывная на сегменте [a, b] функция интегрируема, то для любого положительного числа ε можно указать такое разбиение T сегмента [a, b], что разность S - s < ε, где S и s - соответственно верхняя и нижняя суммы разбиения T. Но S и s равны соответственно Sd и Si, где Sd и Si - площади ступенчатых фигур (многоугольников), первая из которых содержит криволинейную трапецию, а вторая содержится в криволинейной трапеции (на Рис. 2 изображены также и указанные ступенчатые фигуры). Так как Sd - Si < ε, то, в силу теоремы 1, криволинейная трапеция квадрируема. Поскольку предел при Δ → 0 верхних и нижних сумм равен и s ≤ P ≤ S, то площадь P криволинейной трапеции может быть найдена по формуле .
Замечание. Если функция f(x) непрерывна и неположительна на сегменте [a, b], то значение интеграла равно взятой с отрицательным знаком площади криволинейной трапеции, ограниченной графиком функции f(x), ординатами в точках a и b и отрезком оси Ox между точками a и b. Поэтому, если f(x) меняет знак, то равен сумме взятых с определенным знаком площадей криволинейных трапеций, расположенных выше и ниже оси Ox, причем площади первых берутся со знаком “+”, а вторых со знаком “-“.
Дата добавления: 2015-07-30; просмотров: 6563;
