Вычисление объема и площади поверхности тела вращения с помощью определенного интеграла
Пусть дано тело (V), ограниченное замкнутой поверхностью, (X) и (Y) – многогранники объёма X и Y, содержащиеся в (V) и содержащие (V). Очевидно, что существуют V*=Sup{X} и V*=Inf{Y}.
Если V*= V*, то их общее значение V называется объёмом тела (V), а само тело в этом случае называется кубируемым.
Теорема 1: Для того, чтобы тело (V) было кубируемым, необходимо и достаточно, чтобы существовали такие две последовательности многогранников {(An)} и {(Bn)}, содержащихся в (V) и содержащих (V) соответственно, объёмы которых имели бы общий предел: . Тогда этот предел V и будет объёмом тела (V).
Теорема 2: Если для тела (V) можно построить такие две последовательности кубируемых тел {(Qn)} и {(Rn)}, содержащихся в (V) и содержащих (V) соответственно, объёмы которых имеют общий предел: , то тело (V) кубируемо и его объём равен V.
Рассмотрим произвольное тело (V). Пусть нам известна площадь любого его сечения плоскостью, перпендикулярной оси OX.
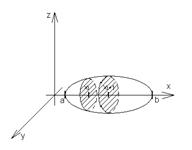
Обозначим a и b – абсциссы крайних сечений. Площадь сечения изменяется вместе с перемещением секущей плоскости, т. е. является функцией от x. Обозначим эту функцию f(x). Будем считать её непрерывной на [a,b]. Предположим также, что любая пара сечений спроектированных на плоскость, перпендикулярную OX, даст фигуры, целиком лежащие одна в другой

При выполнении всех этих условий
Док-во формулы:
Разобьём отрезок [a,b] на части точками a=x0<x1<...<xi<xi+1<...<xn=b. Через эти точки проведём плоскости, перпендикулярные OX. Эти плоскости разобьют тело (V) на n слоёв, толщина которых =Δxi i=0,1,...,n-1. Пусть mi и Mi – наименьшее и наибольшее значение функции P(x) на [xi , xi+1], т. е. площади наименьшего и наибольшего сечений на [xi , xi+1]. Тогда i-й слой содержится между двумя прямыми цилиндрами высотой Δxi , площадь основания которых mi и Mi . Объёмы их mi Δxi и Mi Δxi .
Построим цилиндры для каждого слоя, получим два ступенчатых тела, содержащегося в (V) и содержащего (V), объёмы которых
В силу теоремы 2 получим:
С помощью формулы получаем формулу объёма тела вращения:
Пусть тело (V) получено вращением криволинейной трапеции, ограниченной сверху кривой y=f(x), xЄ[a,b] вокруг оси OX.

P(X)=πf2(x), . Если кривая y=f(x) задана параметрически уравнениями
, то
Если тело получено вращением x=g(y) , yЄ[c,d] вокруг оси OY криволинейной трапеции, то
Площадь поверхности вращения

Рассмотрим спрямляемую кривую y=f(x), xЄ[a,b]. Пусть f(x) непрерывна вместе со своей производной на [a,b] и длина кривой равна S. Если кривую вращать вокруг оси ОХ, то она опишет некоторую поверхность, которую будем называть поверхностью вращения. Найдём её площадь. Дадим сначала определение площади поверхности вращения. Для этого разобьём отрезок [a,b] на n частей точками a=x0<x1<...<xi<xi+1<...<xn=b. Затем впишем в данную кривую ломаную линию с вершинами Mi(xi, yi), i=0,...,n. Вместе с кривой будем вращать эту ломаную, которая опишет поверхность, составленную из n усечённых конусов.
Под площадью поверхности вращения кривой будем понимать конечный предел площади поверхности вращения ломаной при λ→0, где λ=max Δxi
Pn – площадь поверхности вращения ломаной. Площадь боковой поверхности усечённого конуса, образованного из i – го звена ломаной, равна
Получим, что площадь вращения ломаной равна
Чтобы получить интегральную сумму, преобразуем полученное выражение
В формуле первая сумма – это интеграл. Сумма для функции - непрерывна, значит, интегрируема. Первая сумма → . Покажем, что вторая сумма→0 при λ→0. В силу равномерной непрерывности f(x) на [a,b] Ұε>0  δ>0 такое что как только λ<δ, то
δ>0 такое что как только λ<δ, то
|f(xi)-f(ξi)|<ε и |f(xi+1)-f(ξi)|<ε.
|f(xi)+ f(xi+1)-2f(ξi)|≤ |f(xi)-f(ξi)|+ |f(xi+1)-f(ξi)|<2ε
Поскольку величину 2πSε мы можем сделать сколь угодно малой, то вторая сумма →0 при λ→0. Переходя в (5) к пределу при λ→0, получим
Для параметрически заданной кривой x=φ(t), y=ψ(t), tЄ[α,β] получим
Если кривая задана в полярных координатах уравнением r=r(θ), θЄ[α,β], то
Дата добавления: 2015-07-30; просмотров: 4553;
