Смешанное и векторное произведение векторов. Их свойства. Объем параллелепипеда и тетраэдра
Пусть векторы a,b неколлинеарные векторы (линейно-независимые) ориентированного пространства.
Векторным произведением вектора a на b (в указанном порядке) называется вектор c такой, что:
1)|c|=|a|*|b|*sin(a^b) (sin угла между ними)
2) 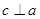 ;
;  (перпендикулярны)
(перпендикулярны)
3)a,b,c – правая тройка векторов
Обозначают векторное произведение: a*b или [a,b]
Замечание: по определению, векторное произведение коллинеарных векторов считается = 0-вектору ( 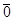 )
)
Теорема: Пусть {i,j,k} правый ортонормированный базис и  имеют координаты: a(a1,a2,a3), b(b1,b2,b3). Тогда их произведение [a,b](|
имеют координаты: a(a1,a2,a3), b(b1,b2,b3). Тогда их произведение [a,b](|  | ,|
| ,| 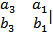 ,|
,|  |)
|)
Свойства векторного произведения векторов:
1)[a,b]=-[b,a]
2)[αa,b]=α[a,b], α-число
[a,βb]=β[a,b]
3)[a+b,c]=[a,b]+[b,c]
[a,b+c]=[a,b]+[a,c]
4)[a,[b,c]]=b(ac)-c(ab), (ab-скалярное произведение векторов)
Докажем 4 свойство. Выберем в пространстве правый ортонормированный базис {i,j,k}, который выберем следующим образом: i=1/|b|*b
j выберем так, чтобы он был перпендикулярен вектору i и имел длину = 1, и 3-ка векторов j,b,c была компланарной
k=[i,j] – векторное произведение (k=1)
В этом базисе: b(b1,0,0); с(с1,с2,0); а(а1,а2,а3)
Вычислим: [b,c]
[b,c](0,0,b1c2)
[a,[bc]](| 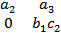 |,|
|,| 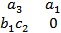 |,
|,  |)
|)
[a,[b,c]](a2b1c2, -a1,b1,c2,0)
ac=a1c1+a2c2+a3*0
ab=a1b1
b(a,c)=(a1b1c1+a2b1c2,0,0)
c(a,b)=(a1b1c1,a1b1c2,0)
((ac)b-(ab)c)(a2b1c2, -a1b1c2,0)
Пусть a,b,c- 3 некомпланарных вектора, ориентированного пространства.
Смешанным произведением векторов a,b,c называется число равное скалярному произведению вектора a на векторное произведение векторов[b,c] (abc или (a,b,c))
Т.о., по определению abc=a[b,c] (1)
Замечание: Если векторы a,b,c компланарны, то по определению их смешанное произведение считается = 0.
Теорема: Пусть векторы a,b,c в правом ортонормированном базисе {i,j,k} имеют координаты a(a1,a2,a3), b(b1,b2,b3), c(c1,c2,c3). Тогда их смешанное произведение: abc=| 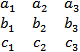 |
|
Док-во:
имеем [b,c](|  | |, |
| |, |  |, |
|, | 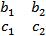 |) (разложим определитель по элементам 1 строки)
|) (разложим определитель по элементам 1 строки)
a*[b,c]=a1| 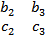 |+a2|
|+a2|  |+a3|
|+a3| 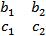 |= a1|
|= a1| 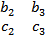 |- a2|
|- a2|  |+ a3|
|+ a3| 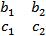 |=|
|=| 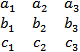 | ч.т.д.
| ч.т.д.
Свойства:
1)abc=-bac=-cba=-acb
2)abc=cab=bca (не меняет знак)
3)(αa)bc=α(abc)
a(βb)c=β(abc)
ab(γc)=γ(abc)
4)(a+d)bc=abc+dbc, также можно представить (a+d)*[bc]=a[bc]+d[bc]
Рассмотрим теперь:
[a,b]*[x,y]=[a,b]xy (смешанное произведение векторов)=-yx[ab]=-y*[x,[a,b]]=-y*(a(xb)-b(x,a))=-(xb)(ya)+(xa)(yb)
x=a, y=b
[a,b]2=a2b2-(ab)2=| | ≥0 определителем Грама
Для любой пары векторов a и b определитель Грама не отрицательный, при чем этот определитель =0 в том и только в том случае, когда векторы a,b-коллинеарны.
Параллелепипедом называется призма, основанием которой служит параллелограмм.
Объем параллелепипеда. Если параллелепипед построен на приведенных к общему началу векторах 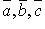 , а
, а  ,
,  ,
,  ,
,  - радиус-векторы его соответствующих вершин
- радиус-векторы его соответствующих вершин  то объем параллелепипеда:
то объем параллелепипеда:

В координатах:

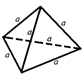
Объем четырехгранной пирамиды (тетраэдра) равен одной шестой объема параллелепипеда, построенного на его сходящихся в одной вершине ребрах. А объем этого параллелепипеда – абсолютная величина смешанного произведения трех векторов, общее начало которых находится в одной из вершин пирамиды, а концы – в остальных трех ее вершинах. Если вершинами пирамиды служат точки M1, M2, M3, M4, то полагая a=M1M2; b=M1M3; c=M1M4, получимV=1/6[a,b,c]
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда: V = So · h
где V - объем параллелепипеда, So - площадь основания, h - длина высоты.

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда: V = a · b · h
где V - объем прямоугольного параллелепипеда, a - длина, b - ширина, h - высота.

Формула объема правильного тетраэдра: 
где V - объем правильного тетраэдра, a - длина ребра правильного тетраэдра.
Дата добавления: 2015-07-30; просмотров: 3521;
