Аффинные преобразования плоскости и их свойства. Группа аффинных преобразований и ее подгруппы. Применение аффинных преобразований к решению задач
Отображение плоскости P в плоскость R — закон или правило, по которому каждой точке плоскости P сопоставлена некоторая определенная точка на плоскости R. Обозначается f: P→R. Если нужно указать, что точке А на плоскости Р соответствует точка В на плоскости R, то напишем B=f(A), в этом случае В — образ точки А, точка А — прообраз точки В. Совсем не обязательно каждая точка плоскости R является образом какой-либо точки. Если для некоторого отображения плоскости P и R совпадают, то такое отображение называется преобразованием плоскости.
Отображение f: P→R называется взаимно однозначным, если каждая точка плоскости R имеет прообраз, и притом только один.
При выбранных системах координат на плоскостях P и R отображение сопоставляет паре чисел (x,y) пару чисел (x',y'). Задать отображение при выбранных СК — всё равно что задать 2 функции, каждая из которых зависит от 2-х независимых переменных: x΄=φ(x,y), y΄=ψ(x,y).
Преобразование f плоскости Р называетсялинейным, если на Р существует такая декартова система координат, в которой f может быть записано формулами: x΄=a1x+b1y+c1, y΄=a2x+b2y+c2. Взаимно однозначное линейное преобразование называется аффинным.
Для того, чтобы преобразование, задаваемое формулами x΄=a1x+b1y+c1, y΄=a2x+b2y+c2, было взаимно однозначным, необходимо и достаточно, чтобы 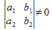 . Таким образом, аффинное преобразование определяется формулами x΄=a1x+b1y+c1, y΄=a2x+b2y+c2 при условии
. Таким образом, аффинное преобразование определяется формулами x΄=a1x+b1y+c1, y΄=a2x+b2y+c2 при условии 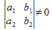 .
.
Геометрические свойства аффинных преобразований:
Рассмотрим на плоскости прямую с уравнением  и найдем её образ при преобразовании f. (Образ прямой — множество образов её точек). Радиус-вектор образа М' произвольной точки М можно вычислить так:
и найдем её образ при преобразовании f. (Образ прямой — множество образов её точек). Радиус-вектор образа М' произвольной точки М можно вычислить так: 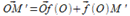 =
=  , где
, где 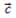 - постоянный вектор
- постоянный вектор 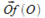 , а
, а 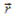 - радиус-вектор точки М. По свойствам линейных преобразований получаем
- радиус-вектор точки М. По свойствам линейных преобразований получаем 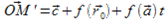 . Так как f – аффинное преобразование, и
. Так как f – аффинное преобразование, и 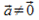 то
то 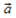 перейдет в вектор
перейдет в вектор 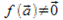 и уравнение
и уравнение 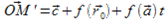 является уравнением прямой линии. Итак, образы всех точек прямой
является уравнением прямой линии. Итак, образы всех точек прямой 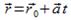 лежат на прямой. F определяет взаимно однозначное отображение одной прямой на другую.
лежат на прямой. F определяет взаимно однозначное отображение одной прямой на другую.
1.При аффинном преобразовании прямая линия переходит в прямую линию, отрезок переходит в отрезок, параллельные прямые переходят в параллельные.
2.При аффинном преобразовании отношение длин параллельных отрезков не изменяется.
Док-во: пусть отрезки АВ и CD параллельны. Это значит, что существует такое число λ, что 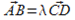 . Образы векторов
. Образы векторов 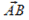 и
и 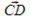 связаны той же зависимостью
связаны той же зависимостью 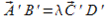 . Отсюда следует, что
. Отсюда следует, что 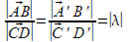 .
.
Следствие. Если точка С делит отрезок АB в некотором отношении λ, то её образ C' делит образ A'B' отрезка АВ в том же отношении λ.
Свойства аффинного преобразования:
1.Образом параллельных прямых являются параллельные прямые
2. При аффинном преобразовании сохраняется отношение двух отрезков, расположенных на одной прямой AB/CD=A΄B΄/C΄D΄
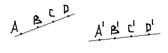
3. При аффинном преобразовании сохраняется отношение параллельных отрезков
4.При аффинном преобразовании угол и отношение произвольных отрезков не сохраняются, так как любой треугольник можно перевести в любой другой. Поэтому высота и биссектриса треугольника преобразуются обычно в другие линии, медиана же переходит в медиану, так как середина отрезка переходит в середину.
5. При аффинном преобразовании параллелограмм переходит в параллелограмм, трапеция в трапецию.
Группа аффинных преобразований.
Теорема: Множество аффинных преобразований плоскости образуют группу.
Док-во: Пусть задано множество аффинных преобразований A={f1, f2,…fn} и композиция двух аффинных преобразований 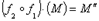 .
. 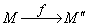 , f – аффинное.
, f – аффинное.
Композиция двух аффинных преобразований есть аффинное преобразование, т.е. операция замкнута на множестве А. 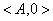
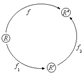
а) eA — нейтральный элемент. 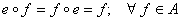 ;
;
б) преобразование, обратное к аффинному также есть аффинное преобразование.
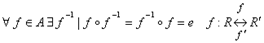
в) 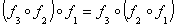
г) группа не является коммутативной т.к. есть примеры того, что два аффинных преобразования дают не коммутативную композицию. Например: 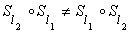
Дата добавления: 2015-07-30; просмотров: 7567;
