Многоугольники. Площадь многоугольника на евклидовой плоскости. Теоремы существования и единственности

Ломанной линией называется конечное упорядоченное множество точек A₁, A₂,…,A_n. Отрезки A_iA_i+1, i=1, 2,…,n-1 называются звеньями ломанной, концы звеньев – вершинами ломанной. Ломанная называется замкнутой, если последняя вершина совпадает с первой. Звенья вида A_i-1A_i, A_iA_i+1 называются смежными звеньями ломанной; у замкнутой ломанной первое и последнее звенья считаются смежными. Ломанная называется простой, если только ее смежные звенья имеют общую точку.

Теорема Жордана. Простая замкнутая ломанная разделяет множество всех точек плоскости на два непересекающихся подмножества. Одно из таких подмножеств не содержит прямых и называется внутренней областью плоскости относительно данной ломанной.

Объединение простой замкнутой ломаной и внутренней области плоскости относительно этой ломаной называется простым многоугольником, при этом ломаную называют границей многоугольника.

Два многоугольника (или просто множества) F и G называются конгруэнтными (равными), если существует движение f такое, что f(F)=G. Обозначение для конгруэнтных многоугольников: F=G.

Многоугольник F называют суммой многоугольников F₁ и F₂ (F=F₁+F₂), если F=F₁UF₂, а пересечение F₁∩F₂ есть простая ломаная

Определение площади многоугольника. Пусть S положительная функция, определенная на множестве всех простых многоугольников, такая, что:

1) из отношения F=G следует равенство S(F)=S(G)

2) если простой многоугольник F есть сумма многоугольников F₁ и F₂, то S(F)= S(F₁)+S(F₂)

3) если P есть квадрат со стороной равной 1, то S(P)=1.

При выполнении этих условий значение функции S(F) называется площадью многоугольника.

Теорема 1: допустим, что площадь S существует. Тогда для прямоугольника F с длинами сторон, равными x и y, его площадь S(F)=xy.

Док-во: Пусть F – прямоугольник с длинами сторон x и y. Предположим, что площадь S(F) зависит от длин его сторон, то есть считаем, что S(F) есть функция x и y: S(F)=f(x,y). Отметим свойства функции f(x,y). Из свойства 3 площади следует, что f(1,1)=1.

Пусть прямоугольник F составлен из прямоугольников F₁ и F₂ (рисунок). Тогда S(F)= S(F₁)+S(F₂) или f(x,y)=f(x₁+x₂,y)=f (x₁,y)+f(x₂,y). аналогичным свойством обладает функция f относительно второй переменной: f(x,y)=f(x,y₁+y₂)=f (x,y₁)+f(x,y₂). Известно, что положительная функция g(x), определенная при всех x>0 и удовлетворяющая свойству аддитивности g(x₁+x₂)=g(x₁)+g(x₂), имеет вид g(x)=xg(1). Поэтому можно записать, что f(x,y)=xf(1,y)=xyf(1,1)=xy.

Следствие: пусть F – трапеция с основаниями a, b и высотой h. Тогда площадь S(F)=(a+b)*h/2.

В частности, если F – треугольник, то S(F)=1*a*h/2

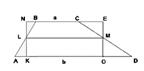
Док-во: пусть ABCD – трапеция, LM – ее средняя линия. Построим прямоугольник NEOK (рисунок). Центральная симметрия с центром в точке L преобразует треугольник NBL в треугольник KAL. Т.к. симметрия есть движение, то ∆NBL=∆KAL. По аксиоме 1 площади S(∆NBL)=S(∆KAL). Аналогично получаем равенство S(∆MCE)=S(∆MDO). По аксиоме 2 площади можно записать: S(ABCD)= S(∆KAL+KLB*CMO+ ∆MDO)= S(∆KAL)+S(KLB*CMO)+ S(∆MDO)= S(∆LNB)+S(KLB*CMO)+S(∆CEM)=S(KNEO)=KO*KH. Т.к. KO=1/2(a+b), то S(ABCD)=1/2(a+b)h.

Единство площади. Допустим, что существуют две функции S и H, определенные на множестве всех многоугольников и удовлетворяющие аксиомам площади. Тогда S=H.

Пусть F – произвольный многоугольник. Представим его каким-нибудь образом как сумму треугольников: F=∆₁+∆₂+…+∆_k. Тогда из теоремы 1 и аксиомы 2 следует, что: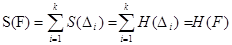

Существование площади. Известно, что скалярное произведение сохраняется при движении в следующем смысле: если A΄, B΄, C΄ - образы точек A, B, C, то: .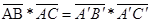

Для доказательства существования площади многоугольника надо построить каким-либо образом положительную функцию на множестве всех многоугольников, удовлетворяющую аксиомам площади. Площадь многоугольника – это результат его измерения с помощью квадратов со сторонами равными 1/n, n=1,2,..

Введем понятие. Пусть AB – сторона многоугольника F, точка MAB. Единичный вектор MN, перпендикулярный стороне AB назовем ортом внешней нормали к стороне AB многоугольника F, если некоторая окрестность вершины луча [MN) не содержит внутренних точек многоугольника F. Другими словами, вектор MN направлен во внешнюю сторону относительно многоугольника.

Теорема: Функция 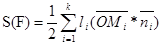, определенная на множестве всех многоугольников, положительна и удовлетворяет всем аксиомам площади. Здесь, F – многоугольник, k – число его сторон, l_i – длина i-й стороны, M_i – внутренняя (не вершина) точка i-ой стороны, n_i – орт внешней нормали i-ой стороны многоугольника F, O – произвольная точка плоскости.

Функция 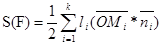не зависит от выбора точки O и точки M_i на i-ой стороне многоугольника.

Проверим для данной функции выполнение аксиом площади:

1.Пусть F=F΄. Существует движение f такое, что f(F)=F΄. Пусть i-ые стороны многоугольников F и F΄ будут соответствующими в отношении f. Пусть O – произвольная точка плоскости, O΄=f(O), точки M_i и M΄_i=f(M_i) принадлежат i-ым сторонам соответствующим многоугольников. Если орт внешней нормали к i-ой стороне многоугольника F обозначить через 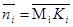, а K΄_i=f(K_i), то вектор 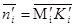будет ортом внешней нормали к i-ой стороне многоугольника F΄, т.к. f – движение и, следовательно, сохраняет скалярное произведение векторов (и угол). Кроме того, длины соответствующих сторон равны: l_i=l΄_i. Отсюда получаем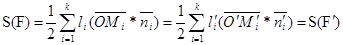

2. Пусть многоугольник F есть сумма многоугольников F₁+F₂. пусть сторона AB – общая для многоугольников F₁ и F₂, векторы 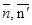- орты внешних нормалей к стороне AB для F₁ и F₂. Тогда 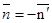, поэтому 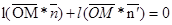. Отсюда получаем: 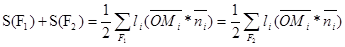. В этих суммах слагаемые, соответствующие общим сторонам многоугольников, взаимно уничтожатся, оставшиеся члены будут соответствовать сторонам многоугольника F.

3. Пусть P=ABCD – квадрат со стороной, равной 1. вычислим S(P). Пусть точка O – центр квадрата, M_i – середины сторон, i=1,2,3,4. Тогда 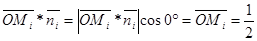, а значение S(P)=1/2(1/2+1/2+1/2+1/2)=1.

Покажем, что S(F)>0 для любого многоугольника F. Любой многоугольник можно представить как сумму треугольников. В силу свойства 2 значение функции S на многоугольнике F будет равно сумме значений функций S на треугольниках. Пусть ABC – треугольник с основанием BC и высотой h, точка M – основание высоты, опущенной из A. Из формулы 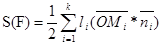предполагая, что точка O совпадает с вершиной A получим, что 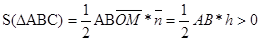. Следовательно, S(F)>0.

Система аксиом Вейля трехмерного евклидова пространства и ее непротиворечивость. Основные понятия евклидова пространства по Вейлю

Пусть V- трехмерное векторное пространство на полем вещественных чисел, а E - непустое множество, элементы которого называются точками. Предположим, что задано отображение σ:E*E→V, и вектор σ(A, B) обозначим через 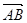. Предполагается также, что дано множество 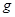отображений, каждое из которых является отображением вида V*V→R.

Множество E называется трехмерным вещественным евклидовым пространством E₃, если выполнены следующие аксиомы.

1.Для каждой из точек А и Е и произвольного вектора 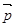из V существует одно и только одна точка Х, такая что .

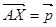2.Для любых точек А, В и С выполняется равенство .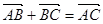

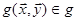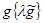3.Множество g является множеством положительно-определенных билинейных форм, таких, что если , то , где 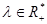. Другими словами, в пространстве V дана положительно-определенная билинейная форма с точностью до положительного числового множителя.

Аксиомы 1-2 определяют структуру трехмерного вещественного аффинного пространства A₃ (с пространством переносов V).

Т.о., базовой структуры евклидова пространства E₃ служит тройка множеств E, V,R, где E-множество точек, V- трехмерное векторное пространство над полем R, а R- поле вещественных чисел.

Следовательно, структура E₃ определяется всего лишь тремя аксиомами Вейля 1-3. Эту систему обозначают через .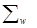

Докажем, что система 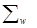непротиворечива. Для этого построим интерпретацию этой системы, используя множество R действительных чисел.

Вектором назовем любой столбец вида 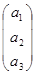, где a_i - произвольные действительные числа. Сумма векторов и умножение векторов определяется как сумма столбцов и умножение столбца на действительное число:

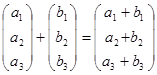и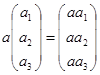

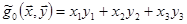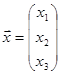Множество g положительно – определенных билинейных форм определим так. Введем в рассмотрение билинейную форму , где и 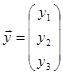, и рассмотрим множество 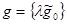, где λ - любое действительное число. Очевидно, что при этом выполняется аксиома 3 Вейля.

Точкой назовем любую строчку вида (m₁, m₂, m₃), где m₁, m₂, m₃ - произвольные действительные числа.

Отображение σ:E*E→V определим так .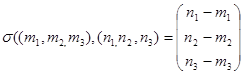

Убедимся в том, что в построенной интерпретации выполняются аксиомы 1 – 2 Вейля.

Аксиома 1. Пусть A=(a₁, a₂, a₃) - произвольная точка, 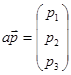- произвольный вектор. Необходимо доказать, что существует одна и только одна точка X=(x₁, x₂, x₃), такая что 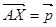, или в терминах нашей интерпретации x_i-a_i=p_i. Ясно, что существует одна и только одна тройка чисел x₁, x₂, x₃ удовлетворяющая этим равенствам, поэтому в построенной интерпретации выполнена аксиома 1.

Аксиома 2. Пусть A=(a₁, a₂, a₃), B=(b₁, b₂, b₃), C=(c₁, c₂, c₃) - произвольные точки. Тогда имеем: , ,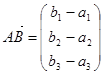

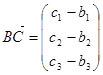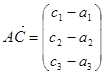
Простым подсчетом убеждаемся в том что .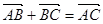

Система аксиом 1 – 3 Вейля непротиворечива, если непротиворечива арифметика вещественных чисел.

Основными объектами геометрии в аксиоматике Вейля являются точка и вектор, а основными отношениями – сумма векторов, произведение вектора на число, откладывание вектора от точки, скалярное произведение векторов. Свойства каждого из этих отношений описываются соответствующей группой аксиом.

Все аксиомы делятся на 5 групп:

1.Аксиомы сложения векторов

2. Аксиомы умножения вектора на действительное число

3. Аксиомы размерности

4. Аксиомы откладывания вектора от точки

5. Аксиомы скалярного произведения

Аксиомы первых трех групп определяют двумерное линейное (или векторное) пространство. Аксиомы первых четырех групп определяют двумерное аффинное пространство. Аксиомами всех пяти групп определяется двумерное евклидово пространство. Т.о., евклидова геометрия строится на базе аффинной путем введения метрики (меры длины и меры угла) с помощью скалярного произведения векторов.