Многогранники. Теорема Эйлера о многогранниках. Топологически правильные и неправильные многогранники
Многогранниками называются тела, поверхности которых состоят из конечного числа многоугольников, называемых гранями многогранника. Стороны и вершины этих многоугольников называются соответственно ребрами и вершинами многогранника.
Многогранники делятся на: выпуклые и невыпуклые.
Выпуклыммногогранником называется такой многогранник, что если взять плоскость любой его грани, то весь многогранник окажется по одну сторону от этой плоскости.
Выпуклые многогранники делятся на: правильные и неправильные.
Правильный многогранник – выпуклый многогранник с максимально возможной симметрией.
Многогранник называется правильным, если:
-он выпуклый;
- все его грани являются равными правильными многоугольниками;
- в каждой его вершине сходится одинаковое число ребер.
Выпуклый многогранник называется топологически правильным, если его гранями являются многоугольники с одним и тем же числом сторон и в каждой вершине сходится одинаковое число граней.
Например, все треугольные пирамиды являются топологически правильными многогранниками, эквивалентнымимежду собой. Все параллелепипеды также являются эквивалентными между собой топологически правильными многогранниками.Четырехугольные пирамиды не являются топологически правильными многогранниками.
Сколько же существует не эквивалентных между собой топологически правильных многогранников.
Существует 5 правильных многогранников:
Тетраэдр – составлен из 4 равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских углов при каждой вершине=180°. Т.о., тетраэдр имеет 4 грани, 4 вершины и 6 ребер.
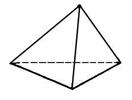
Куб –составлен из 6 квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов при каждой вершине=270°. Т.о., куб имеет 6 граней, 8 вершин и 12 ребер.

Октаэдр –составлен из 8 равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма плоских углов при каждой вершине=240°. Т.о., октаэдр имеет 8 граней, 6 вершин и 12 ребер.
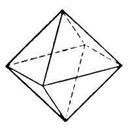
Икосаэдр –составлен из 20 равносторонних треугольников. Каждая его вершина является вершиной 5 треугольников. Сумма плоских углов при каждой вершине=300°. Т.о., икосаэдр имеет 20 граней, 12 вершин и 30 ребер.
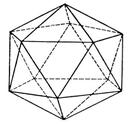
Додекаэдр –составлен из 12 равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских углов при каждой вершине=324°. Т.о., додекаэдр имеет 12 граней, 20 вершин и 30 ребер.
Правильные многогранники также называются платоновыми телами. Каждый из правильных многогранников Платон ассоциировал с 4 «земными» стихиями: земля (куб), вода (икосаэдр), огонь (тетраэдр), воздух (октаэдр), а также с «наземным» элементом – небом (додекаэдр).
Казалось бы, топологически правильных многогранников должно быть гораздо больше. Однако оказывается, что никаких других топологически правильных многогранников, не эквивалентных уже известным правильным, не существует.
Для доказательства этого воспользуемся теоремой Эйлера.
Теорема Эйлера для многогранников – теорема, устанавливающая связь между числами вершин, ребер и граней для многогранников, топологически эквивалентных сфере:
«Сумма числа граней и вершин = числу ребер, увеличенному на 2» - Г+В=Р+2 (данная формула верна для любых выпуклых многогранников).
Пусть дан топологически правильный многогранник, гранями которого являются n - угольники, и в каждой вершине сходится m ребер. Ясно, что n и m больше или равны трем. Обозначим, как и раньше, В - число вершин, Р - число ребер и Г - число граней этого многогранника. Тогда
nГ = 2P; Г =2P/n; mB = 2P; В = 2P/m.
По теореме Эйлера, В - Р + Г = 2 и, следовательно, 2P/m-P+2P/n=2
Откуда Р = 2nm/(2n+2m-nm).
Из полученного равенства, в частности, следует, что должно выполняться неравенство 2n + 2m – nm > 0, которое эквивалентно неравенству (n – 2)(m – 2) < 4.
Найдем всевозможные значения n и m, удовлетворяющие найденному неравенству, и заполним следующую таблицу
| n m | |||
| B=4, Р=6, Г=4 тетраэдр | В=6, Р=12, Г=8 октаэдр | В=12, Р=30, Г=20 икосаэдр | |
| В=8, Р=12, Г=4 куб | Не существует | Не существует | |
| В=20, Р=30, Г=12 додекаэдр | Не существует | Не существует |
Например, значения n = 3, m = 3 удовлетворяют неравенству (n – 2)(m – 2) < 4. Вычисляя значения Р, В и Г по приведенным выше формулам, получим Р = 6, В = 4, Г = 4.
Значения n = 4, m = 4 не удовлетворяют неравенству (n – 2)(m – 2) < 4 и, следовательно, соответствующего многогранника не существует.
Из этой таблицы следует, что возможными топологически правильными многогранниками являются только правильные многогранники (тетраэдр, куб, октаэдр, икосаэдр, додекаэдр).
Анализ учебных планов и программ по математике
Содержание школьного курса математики
Школьным учебным планом на изучение математики с 1 по 11 класс отводится около 2000 учебных часов. Дополнительные часы на изучение математики предусматриваются в системе факультативных курсов (8-11 классы).
Нормативным, обязательным для выполнения документом, определяющим основное содержание школьного курса математики, объем подлежащих усвоению учащимися каждого класса знаний, приобретаемых умений и навыков, явл. учебная программа.
Учебная программа школы основывается на принципах соответствия программы основным целям школы, обеспечивает преемственность получаемой учащимися подготовки в 1-3 классах (нач. школа), 5-9 классах, 10-11 классах.
Учащиеся, которые после окончания девятилетней школы будут завершать среднее образование в системе профессиональнотехнических училищ, в средних специальных учебных заведениях, в вечерних (заочных) школах, должны получить математическую подготовку в том же объеме, что и учащиеся, оканчивающие среднюю общеобраз. школу. Т.о., все учащиеся, получившие среднее образование, приобретают равную возможность для продолжения образования.
Предусмотренное программой содержание школьного математического образования, несмотря на происходящие в нем изменения, в течение достаточно длительного времени сохраняет свое основное ядро. Такая устойчивость основного содержания программы объясняется тем, что математика, приобретая в своем развитии много нового, сохраняет и все ранее накопленные научные знания, не отбрасывая их как устаревшие и ставшие ненужными.
"Ядро" современной программы по математике составляют:
1. Числовые системы. 2. Величины.
3. Уравнения и неравенства. 4. Тождественные преобразования математических выражений.
5. Координаты. 6. Функции.
7. Геометрические фигуры и их свойства. Измерение геометрических величин. Геометрические преобразования. 8. Векторы.
9. Начала математического анализа. 10. Основы информатики и вычислительной техники.
Каждый из вошедших в это "ядро" разделов имеет свою историю развития как предмет изучения в средней школе. На каком возрастном этапе, в каких классах, с какой глубиной и при каком числе часов изучаются эти разделы, определяет программа по математике для средней школы.
Раздел "Числовые системы" изучается на протяжении всех лет обучения. В школьную программу вопросы числовых систем входили уже давно. Но с течением времени происходило снижение возраста, в котором учащиеся изучали включаемые в программу темы, возрастала глубина их изложения. В наст время изыскиваются возможности включения в программу заключительной темы этого раздела - "Комплексные числа".
Изучение величин в программах и учебниках по математике не выделено в специальный раздел. Но на протяжении всех лет обучения учащиеся выполняют действия с различными величинами при решении задач, особенно задач, отражающих связи курса математики с дисциплинами естественнонаучного, технического циклов.
Изучению уравнений и неравенств посвящается значительная часть всего учебного времени. Особая значимость темы состоит в широком применении уравнений и неравенств в самых различных областях приложений математики. До недавнего времени систематическое изучение уравнений начиналось лишь с 7 класса. В течение последних десятилетий знакомство с уравнениями и применение уравнений к решению задач вошло в курс математики начальной школы и 5-6 классов.
Выполнение тождественных преобразований, овладение специфическим языком математики требуют от учащихся не только понимания, но и отработки прочных практических навыков на достаточно большом числе тренировочных упражнений. Такие упражнения, содержание которых в каждом разделе курса обладает своими особенностями, выполняются учащимися всех классов.
Координаты и функции вошли в курс математики средней школы только в первой четверти XX в. Характерной особенностью современного школьного курса математики являются расширение этих разделов и возрастающая роль метода координат и функций в изучении других тем школьной программы.
Наибольшую остроту в обсуждении вопросов его содержания приобрел в последние десятилетия курс геометрии. Здесь в значительно больших размерах, чем в других разделах школьного курса математики, возникли проблемы соотношения традиционного содержания с необходимыми новыми дополнениями. Однако при всех различиях в подходах к решению этой проблемы получило общее одобрение включение в курс геометрических преобразований.
Векторы впервые вошли в курс геометрии нашей школы только в середине 70-х годов. Большая общеобразовательная значимость этой темы, обширные практические применения обеспечили ей общее признание. Однако вопросы доходчивого для всех учащихся изложения этого раздела в школьных учебниках, применения векторов к решению содержательных задач находятся еще в стадии разработки и могут найти свое решений только на основе глубокого анализа и учета результатов школьного преподавания.
Элементы математического анализа вошли в программу общеобразовательной школы недавно. Включение в программу этих разделов вызвано их большой прикладной значимостью.
Раздел основы информатики и вычислительной техники отражает требования, предъявляемые к современной математической подготовке молодежи в связи с широким внедрением в практику ЭВМ.
Дата добавления: 2015-07-30; просмотров: 19531;
