Вторая теорема Больцано-Коши

Теорема 2. Пусть функция 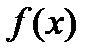определена и непрерывна на 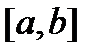, , 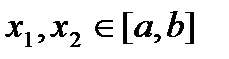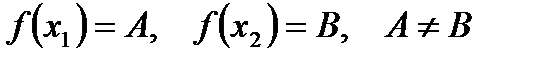. Тогда для 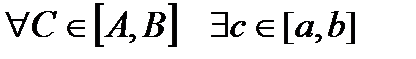, что

.

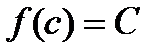Доказательство. Пусть для определенност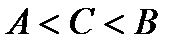и (если 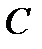совпадает 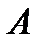с или с 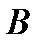, тогда как можно взять или 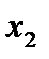- все доказано).

Построим вспомогательную функцию

.

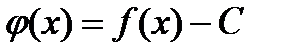Рассмотрим ее на 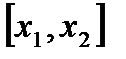. На этом сегменте 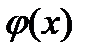- непрерывна, потому что является разностью двух непрерывных функций и 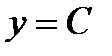, к тому же:

,

,

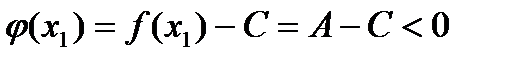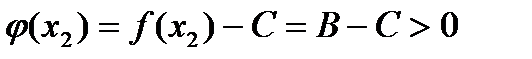т.е. на концах сегмента 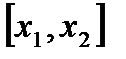функция 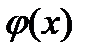принимает значения разных знаков. Тогда по предыдущей теореме 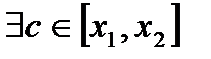, что 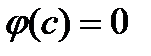, т.е. 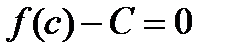, а тогда 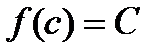, что и нужно было доказать.

Следствие. Пусть функция 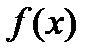определена и непрерывна на 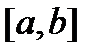, тогда множество ее значений - сегмент.

Доказательство. По второй теореме Вейерштрасса 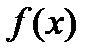достигает на 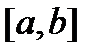своих супремума и инфимума. Обозначим:

.

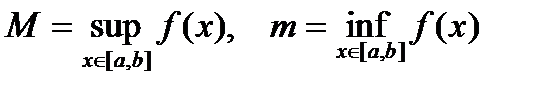Тогда

;

.

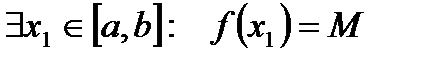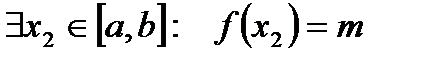По второй теореме Больцано-Коши функция 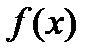принимает все промежуточные значения, которые находятся между 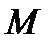и 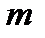, то есть областью значений 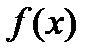является сегмент 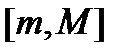, что и нужно было доказать.

Вопросы

1. Может ли непрерывная на сегменте функция не принимать нулевого значения ни в одной точке сегмента? Ответ объяснить.

2. Может ли непрерывная на интервале функция не принимать нулевого значения ни в одной точке сегмента? Ответ объяснить.

3. Пусть функция 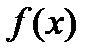определена и непрерывна на 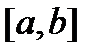, а на концах сегмента принимает значения одного знака. Вытекает ли из этого, что функция не принимает нулевого значения ни в одной точке сегмента? Ответ объяснить.

4. Пусть функция 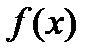определена и непрерывна на 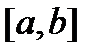, а на концах сегмента принимает значения разных знаков. Вытекает ли из этого, что функция принимает нулевое значение в какой-то точке сегмента? Ответ объяснить.

5. Доказать первую теорему Больцано-Коши.

6. Доказать, не решая уравнение непосредственно, что уравнение 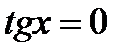обязательно будет иметь корень на сегменте .

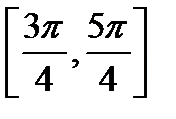7. Пусть функция 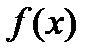определена и непрерывна на 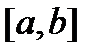, а на концах сегмента принимает значения разных знаков. Сколько корней может иметь уравнение 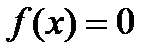? Ответ объяснить.

8. Пусть функция 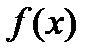определена на 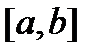, а множество ее значений – это 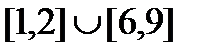. Что можно сказать о непрерывности 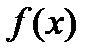на 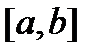? Почему?

9. Доказать вторую теорему Больцано-Коши.

10. Доказать следствие из второй теоремы Больцано-Коши.