Вторая (обратная) задача динамики МТ
Вторая задача динамики МТ заключается в том, что, зная массу МТ и действующие на нее силы, необходимо определить уравнения или кинематические параметры ее движения при определенном способе задания движения.
Вторая задача динамики решается, используя соотношения (1.6) – (1.8), в зависимости от способа задания движения (в основном используется операция интегрирования).
Задачи динамики для несвободной МТ достаточно часто сводятся к тому, чтобы, зная массу МТ и действующие на нее активные силы (заданные силы), определить уравнения или кинематические параметры ее движения и пассивные силы (реакции связи), т. е. одновременно решаются первая и вторая задачи динамики.
Силы, приложенные к МТ, могут зависеть от времени, положения МТ в пространстве и от скорости ее движения, т. е.
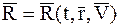 .
.
Рассмотрим решение второй задачи в декартовой системе координат. Правые части дифференциальных уравнений движения (1.7) в общем случае содержат функции времени, координат, их производных по времени:
 (1.9)
(1.9)
Для того, чтобы найти уравнения движения МТ в декартовых координатах, необходимо дважды проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка (1.9), в которых неизвестными функциями являются координаты движущейся МТ, а аргументом – время t. Из теории обыкновенных дифференциальных уравнений известно, что общее решение системы трех дифференциальных уравнений второго порядка содержит шесть произвольных постоянных:
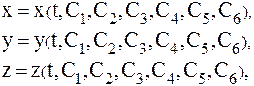 (1.10)
(1.10)
где Cg, (g = 1,2,…,6) – произвольные постоянные.
Продифференцировав соотношения (1.10) по времени, определим проекции скорости МТ на координатные оси:
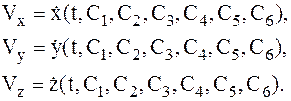 (1.11)
(1.11)
В зависимости от значений постоянных Cg, (g =1,2,…,6) уравнения (1.10) описывают целый класс движений, который могла бы совершить МТ под действием данной системы сил.
Действующие силы определяют только ускорение МТ, а скорость и положение МТ на траектории зависят еще от скорости, которую сообщили МТ в начальный момент, и от начального положения МТ.
Для выделения конкретного вида движения МТ (т. е. чтобы сделать вторую задачу определенной) надо дополнительно задать условия, позволяющие определить произвольные постоянные. В качестве таких условий задают начальные условия, т. е. в какой-то определенный момент времени, принимаемый за начальный, задаются координаты движущейся МТ и проекции ее скорости:
при t = t0(t = 0)
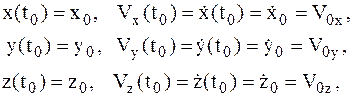 (1.12)
(1.12)
где 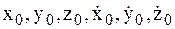 – значения координат МТ и их производных в начальный момент времени t0.
– значения координат МТ и их производных в начальный момент времени t0.
Используя начальные условия (1.12), формулы (1.10) и (1.11), получаем шесть алгебраических уравнений для определения шести произвольных постоянных:
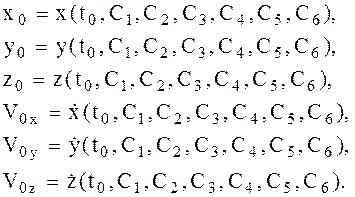 (1.13)
(1.13)
Из системы (1.13) можно определить все шесть произвольных постоянных:
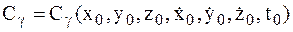 . (g = 1,2,…,6)
. (g = 1,2,…,6)
Подставляя найденные значения Cg, (g = 1,2,…,6) в уравнения движения (1.10), находим решения системы (1.9).
При движении МТ в плоскости Оху имеются два дифференциальных уравнения движения. При их интегрировании появятся четыре произвольные постоянные, которые определяются из начальных условий.
В случае прямолинейного движения МТ имеется только одно дифференциальное уравнение. При его интегрировании появятся две произвольные постоянные, которые определяются из начальных условий.
Задача интегрирования системы дифференциальных уравнений (1.9) при заданных начальных условиях в общем случае является достаточно сложной и не всегда разрешимой в элементарных функциях.
В случаях, когда сила зависит или только от времени (например, периодически изменяющаяся сила, вызывающая колебания) или только от положения МТ (например, ньютонова сила тяготения) или только от скорости движения МТ (например, сила сопротивления среды) или постоянна, вторая задача динамики чаще всего может быть решена достаточно просто (примеры приведены в параграфе 1.4).
Дата добавления: 2015-08-01; просмотров: 2532;
