Пример 1. 2 Движение свободной МТ массы m задано уравнениями

2 Движение свободной МТ массы m задано уравнениями

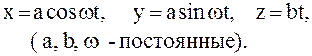
Определить силу 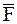, действующую на МТ, как функцию ее координат.

3n = 1 4ПЗД – да

5Векторный способ – нет.

6Координатный декартовый способ – да.

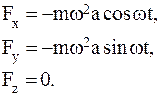
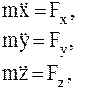
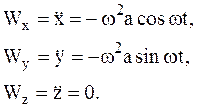
9Ответ: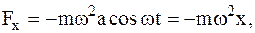

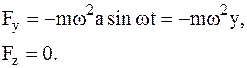
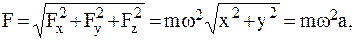
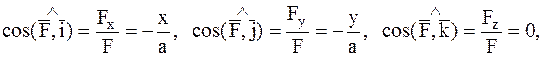
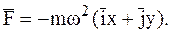
Пример 2 (обратная задача примера 1).

2 На свободную МТ массы m действует сила, проекции которой на координатные оси:

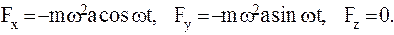
Определить уравнения движения МТ, если в начальный момент она имеет координаты (а,0,0) и ей сообщили скорость .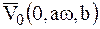

3 n = 1 4 ПЗД – нет. ВЗД – да.

5Векторный способ – нет.

6 Координатный декартовый способ – да.

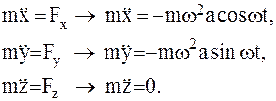
Каждое из уравнений 6интегрируется дважды:

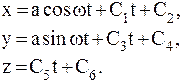
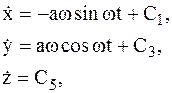
Постоянные интегрирования С₁,С₂,…С₆ находятся из начальных условий, наложенных на МТ:

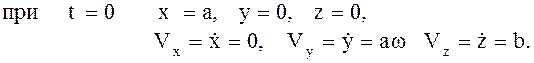
Используя начальные условия, получим систему шести уравнений для определения шести постоянных интегрирования, решение которой имеет вид:

С1= 0, С2 = 0, С3 = 0, С4 = 0, С5 = b, С6 = 0.

9 Ответ: уравнения движения примут вид:

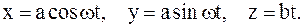
Пример 3 (движение МТ в плоскости)

2Определить уравнение движения снаряда массы m в свободном полете в однородном поле силы тяжести, выпущенного самолетом с высоты h над землей с абсолютной скоростью, равной 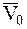, направленной горизонтально, принимая силу сопротивления воздуха равной .

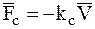Используется декартовая система координат: ось х направлена по горизонтали, ось у – по вертикали.

Снаряд принимается за МТ. Силовая схема изображена на рис. 2, где .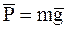

3 n = 1 4ПЗД – нет. ВЗД – да.

5Векторный способ – нет.

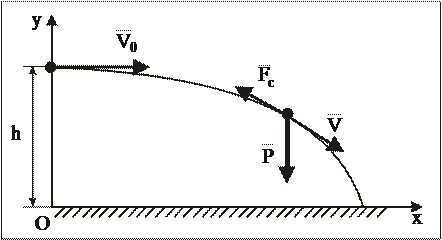
Рис. 2

6 Координатный декартовый способ – да.

® ,

® .

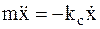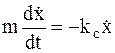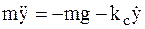Проинтегрируем каждое из уравнений дважды.

Разделяя переменные, получим:

, .

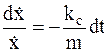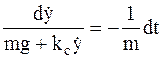Интегрируя первый раз, найдем:

, .

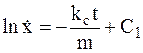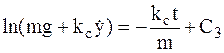Потенцируя эти выражения, получим:

, .

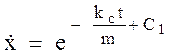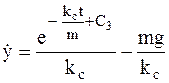Интегрируя второй раз, найдем:

, .

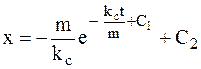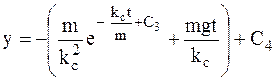Используя начальные условия,

при t=0, x=0, y=h, , ,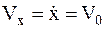

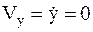получим систему четырех алгебраических уравнений для четырех неизвестных постоянных интегрирования С₁, С₂, С₃, С₄:

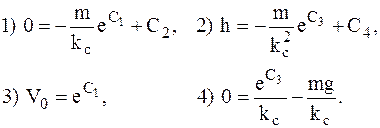
Из четвертого уравнения С₃ = ln mg,

из третьего уравнения С₁ = ln V₀,

из второго уравнения ,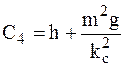

из первого уравнения .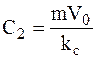

9 Ответ: уравнения движения примут вид:

, .

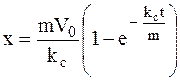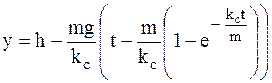Время полета снаряда до земли может быть найдено из второго соотношения, положив в нем y=0. Дальность полета снаряда может быть определена из первого соотношения, подставив в него время t полета снаряда до земли.

Пример 4(математический маятник)

2 МТ массы m, подвешенная на невесомой нерастяжимой нити (стержне) длины l к неподвижной точке О, совершает под действием собственного веса движение по окружности в вертикальной плоскости около положения равновесия (плоский математический маятник).

Найти закон движения МТ для случая ее малых отклонений от положения равновесия и натяжение нити (стержня) N как функцию угла j, образованного нитью с вертикалью (рис. 3), если при t = 0 j = j₀ и V = V₀.

3n = 3

n = 1

4ПЗД – нет, ВЗД – да.

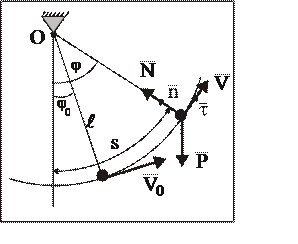
Рис. 3

5 Векторный способ – нет.

6Координатно-декартовый способ – нет.

7Естественный способ – да.

Траектория движения МТ известна (окружность), поэтому используются уравнения движения МТ при естественном способе задания движения (1.8):

,

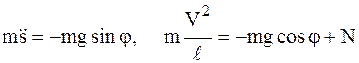так как .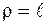

Имея в виду, что 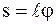, перепишем эти уравнения в виде:

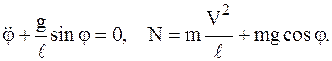
Интегрируя первое уравнение, можно решить ВЗД – найти угол j как функцию от времени t, то есть закон движения МТ.

Второе уравнение дает нам возможность решить ПЗД – определить натяжение нити (стержня) N.

Для того, чтобы найти закон движения МТ – решить ВЗД, необходимо проинтегрировать дважды дифференциальное уравнение движения (первое уравнение), что невозможно сделать через элементарные функции. Поэтому найдем приближенное решение задачи. Для этого будем рассматривать малые отклонения МТ от положения равновесия, принимая .

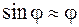Тогда дифференциальное уравнение движения примет вид:

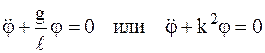, где .

Общее решение этого линейного дифференциального уравнения с постоянными коэффициентами можно представить в следующем виде:

,

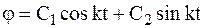где С₁ и С₂ – произвольные постоянные интегрирования, определяемые из начальных условий движения: , .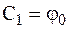

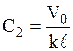9 .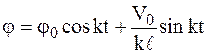

Движение МТ является гармоническим колебательным движением с периодом колебаний

.

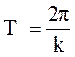
Таким образом, период малых колебаний математического маятника не зависит от массы МТ и начальных условий, а зависит только от длины математического маятника.

n = 2

4ПЗД – нет. ВЗД – да. 5 Векторный способ – нет.

6Координатно-декартовый способ – нет.

7Естественный способ – да.

Для того, чтобы проинтегрировать первое уравнения преобразуем это уравнение, подставив 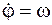, а также 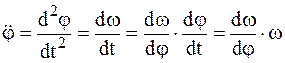в первое уравнение. Тогда, разделив переменные, получим:

.

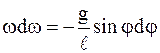Проинтегрировав это уравнение, будем иметь:

,

где С – произвольная постоянная интегрирования.

Использовав начальные условия при 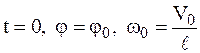, найдем постоянную интегрирования С:

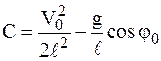, и, следовательно,

.

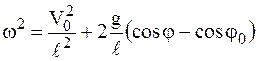Умножив обе части этого выражения на 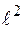, получим

.

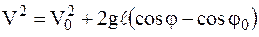n = 3

4 ПЗД – да. 5 Векторный способ – нет.

6Координатно-декартовый способ – нет.

7Естественный способ – да.

Подставляя формулу для 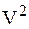во второе уравнение движения, найдем натяжение нити (стержня) N как функцию j:

.

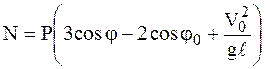Из полученной формулы можно сделать следующие выводы:

· если j₀ = 0 (маятнику сообщается начальная скорость 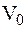в положении равновесия МТ), то натяжение нити (стержня) определяется формулой:

,

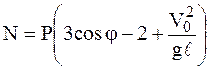причем в самом нижнем положении точки (при j = 0) натяжение нити (стержня) будет:

;

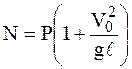· если маятник отвести от вертикали на угол j₀ и затем отпустить его без начальной скорости (V₀ = 0), то натяжение нити (стержня) будет определяться соотношением:

.

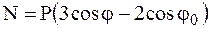Очевидно, что если j₀=180⁰, то в самом нижнем положении МТ (при j = 0) натяжение нити (стержня) N будет в пять раз больше веса Р.