Колебательное движение МТ в среде без сопротивления при отсутствии возмущающей силы
В этом случае n=0, h=0 и общее решение (1.23) примет вид:
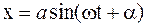 , (1.24)
, (1.24)
где а и a – постоянные интегрирования, которые находятся из начальных условий.
МТ перемещается по закону синуса (или косинуса). Такое движение носит название простого гармонического колебания, график его представлен на рис. 6.
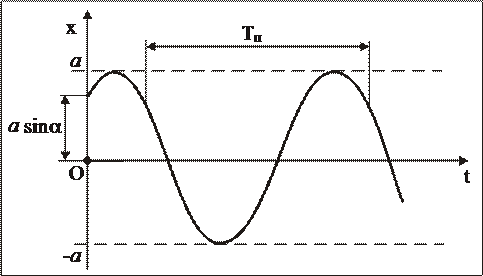
Рис. 6
Скорость этого гармонического колебания МТ будет:
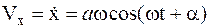 . (1.25)
. (1.25)
Так как 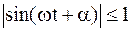 , то постоянная а определяет наибольшее отклонение МТ от центра колебаний О и называется амплитудой колебаний МТ. Параметр
, то постоянная а определяет наибольшее отклонение МТ от центра колебаний О и называется амплитудой колебаний МТ. Параметр 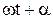 определяет положение МТ и ее скорость в каждый момент времени и называется фазой колебаний, а постоянная α – начальной фазой.
определяет положение МТ и ее скорость в каждый момент времени и называется фазой колебаний, а постоянная α – начальной фазой.
На основании уравнения (1.24) можно сделать вывод, что движение МТ является периодическим. Периодом колебаний называется промежуток времени T, в течение которого МТ совершает одно полное колебание, т.е. МТ в момент времени t + T должна прийти в то же положение х и иметь ту же скорость 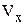 , что и в момент времени t:
, что и в момент времени t:
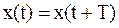 ,
, 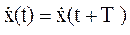 .
.
Наименьшее значение t, при котором выполняются эти условия, определяются равенством 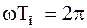 , откуда
, откуда
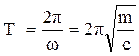 .
.
Величина обратная периоду, определяет число колебаний, совершаемых МТ за одну секунду, и ее называют частотой колебаний:
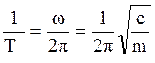 .
.
Соответственно параметр ω называется круговой частотой колебаний. Необходимо отметить, что частота и период колебаний МТ от начальных условий не зависят.
Дата добавления: 2015-08-01; просмотров: 768;
