С сопротивлением при отсутствии возмущающей силы

В этом случае h = 0 и решение может быть представлено формулами (1.18) – (1.20) так как х = х₁.

При малом сопротивлении среды (n < w) в соответствии с формулой (1.18):

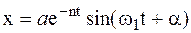, (1.26)

где а и a – постоянные интегрирования, которые находятся из начальных условий.

Из уравнения (1.26) следует, что движение МТ будет колебательным. Эти колебания называют затухающими, так как за счет множителя 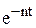размахи колебаний будут убывать, стремясь с течением времени к нулю.

Период затухающих колебаний

.

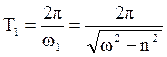Графически затухающие колебания можно иллюстрировать затухающей синусоидой (рис. 7).

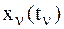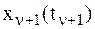Чтобы установить закон затухания размахов колебания, отметим, что промежуток времени между двумя последовательными максимальными отклонениями МТ и равен периоду Т₁, т.е. 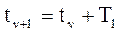. С учетом этого найдем:

.

Отсюда следует, что наибольшие отклонения МТ убывают с течением времени по закону геометрической прогрессии, знаменатель которой 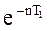называется декрементом колебаний.

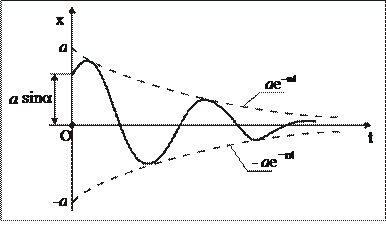Риc.7

Соответственно величина 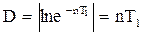называется

логарифмическим декрементом затухания.

В случае большого сопротивления среды (n > w) движение МТ будет неколебательным (апериодическим) затухающим – формула (1.19):

,

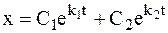где 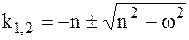– действительные отрицательные числа, а С₁ и С₂ - постоянные интегрирования, которые находятся из начальных условий.

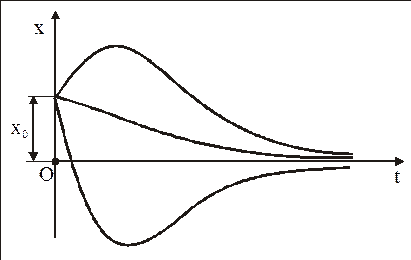
График этого движения МТ в зависимости от величины и знака начального отклонения х₀ и направления начальной скорости 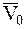имеет форму одной из кривых, изображенных на рис. 8 (или им симметричных относительно оси абсцисс).

+

Рис. 8

В предельном случае (n = w) движение МТ также будет неколебательным (апериодическим) затухающим – формула (1.21):

,

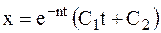где С₁ и С₂ – постоянные интегрирования, которые находятся из начальных условий.

Картина движения МТ будет качественно такой же, как показанная на рис. 8.