Алгоритм решения основной задачи динамики
1. Составить дифференциальные уравнения движения. Для этого необходимо:
а) выбрать координатные оси, поместив их начало в начальном положении точки (если движение прямолинейное, то одну из координатных осей следует проводить вдоль линии движения точки);
б) изобразить движущуюся точку в произвольный момент времени t и показать на рисунке все действующие на нее силы, в том числе и реакции связей (если они есть);
в) найти сумму проекций всех сил на выбранные оси и подставить в уравнения движения.
2. Проинтегрировать полученные уравнения.
3. Установить начальные условия движения точки М и по ним определить константы интегрирования.
4. Из полученных уравнений определить искомые величины.
Пример. Груз массой m сброшен без начальной скорости с самолета, движущегося горизонтально со скоростью V0. Определить уравнение движения груза, если при его движении действует сила сопротивления 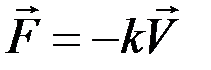 , где k – положительный коэффициент.
, где k – положительный коэффициент.
Решение:

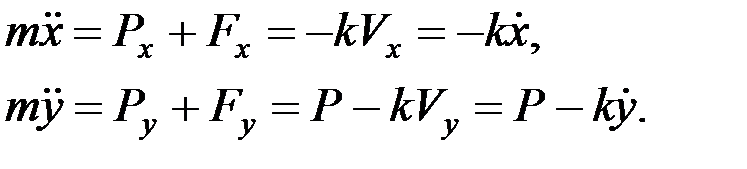
Разделяем переменные, вводя следующую замену:
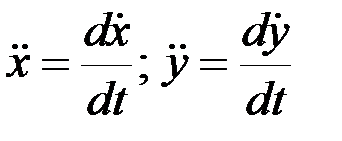 .
.
Интегрируя, получим:
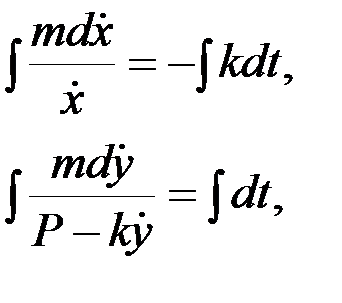
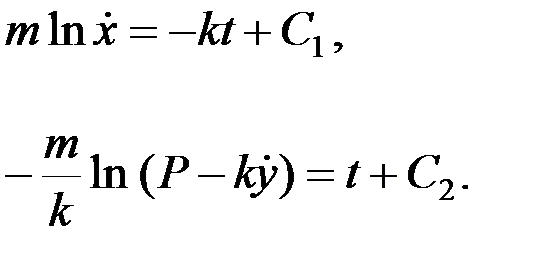
Начальные условия:
при 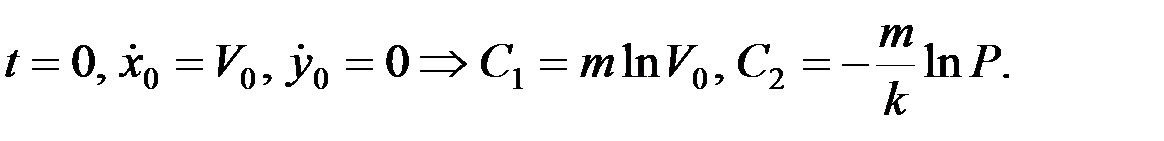
Тогда 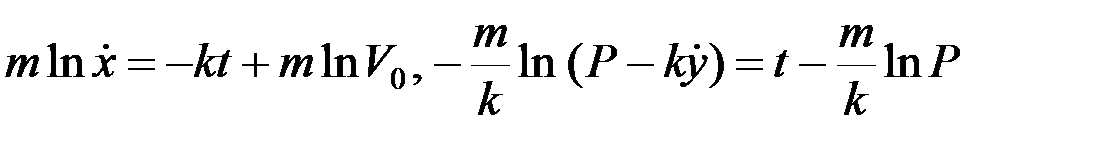 .
.
Интегрируем еще раз:
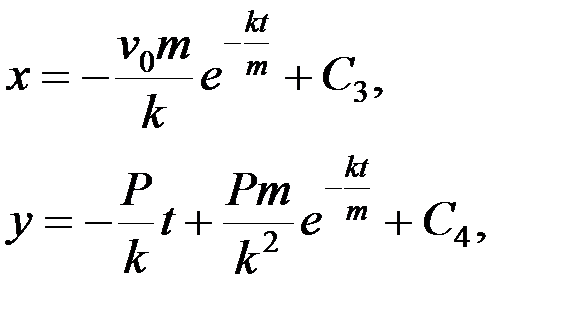
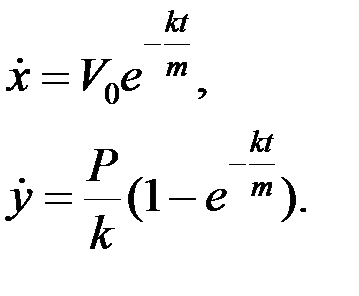
Начальные условия: t = 0; x = 0; y = 0, тогда 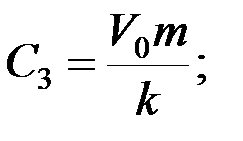

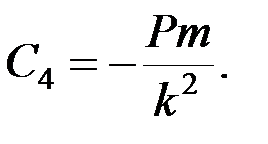
Таким образом, находим искомые уравнения:
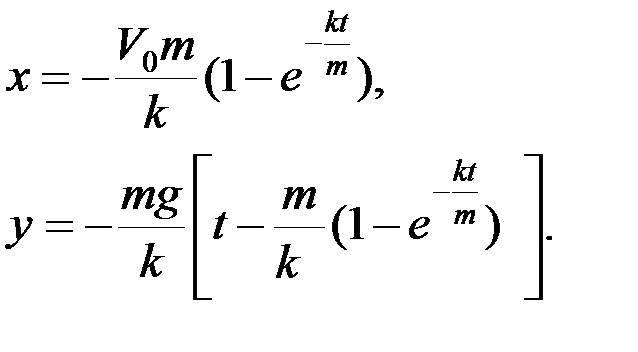
Дата добавления: 2015-08-08; просмотров: 2095;
