Дифференциальные уравнения движения точки

Из кинематики известно, что в прямоугольных декартовых координатах движение точки задается уравнениями:

x = f₁ (t), y = f₂ (t), z = f₃ (t).

Рассмотрим материальную точку, движущуюся под действием сил F₁, F₂ ... F_n. Проецируем равенство 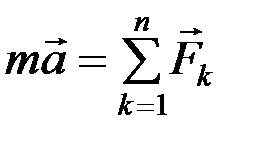на оси x, y, z. Учитывая, что 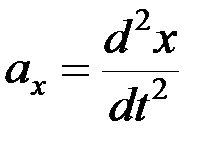, , 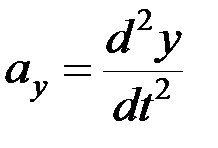, 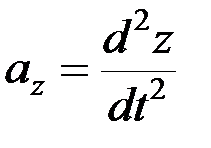получим , , .

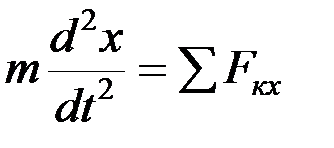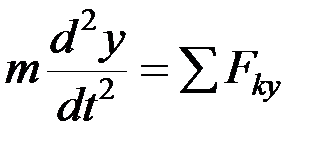Это и есть дифференциальные уравнения движения точки в декартовых координатах. Силы в правых частях уравнений в общем случае могут зависеть от координат x, y, z, от скоростей 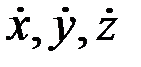или от времени t.