Лекция 9 ДИНАМИКА МЕХАНИЧЕСКОЙ СИСТЕМЫ
Механическая система. Масса системы. Центр масс и его координаты. Теорема о движении центра масс. Свойства внутренних и внешних сил. Дифференциальные уравнения движения центра масс. Осевые моменты инерции тела
 Механической системой называют систему материальных точек. Представим себе механическую систему
Механической системой называют систему материальных точек. Представим себе механическую систему 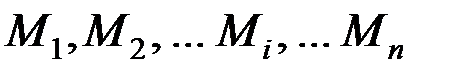 и обозначим координаты i-й точки через xi, yi, zi.
и обозначим координаты i-й точки через xi, yi, zi.
Геометрическая точка С, определяемая координатами:
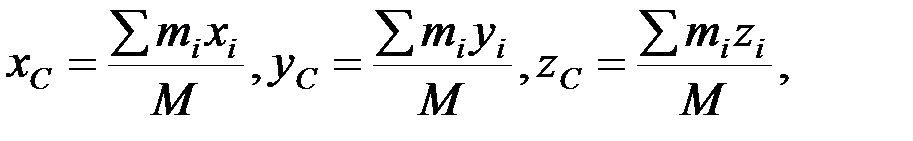 (1)
(1)
где M = åmi – масса всей системы называется центром инерции или центром масс системы. Умножив числитель и знаменатель в этих формулах на ускорение свободного падения g, получим выражения:
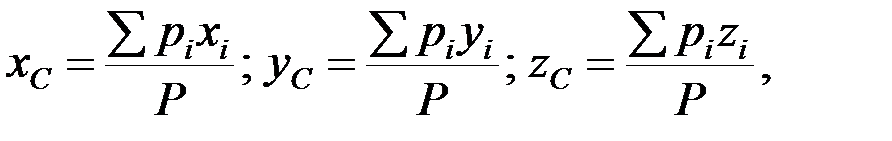
где Р – вес системы.
Очевидно, что центр инерции (ЦИ) совпадает с центром тяжести (ЦТ) системы. Понятие ЦИ гораздо шире, чем понятие ЦТ, т.к. ЦТ существует только, когда система находится в поле сил гравитации, а существование ЦИ не зависит от действия на систему каких-либо сил.
Положение центра инерции может быть также определено значением радиуса-вектора, проведенного в центр инерции из начала координатных осей. Обозначим радиус-векторы точек системы 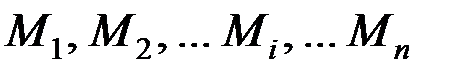 через
через 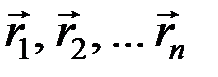 , тогда
, тогда
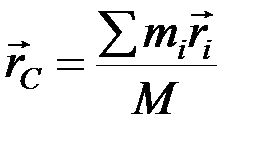 . (2)
. (2)
Это векторное равенство равносильно предыдущим трем, т.к., проецируя обе части равенства (2) на координатные оси, получим равенство (1).
Дата добавления: 2015-08-08; просмотров: 832;
