Дифференциальные уравнения в проекциях на оси естественного трехгранника
Для получения уравнений движения материальной точки на плоскости спроецируем основное уравнение динамики на оси естественного трехгранника t, n, b. Зная, что 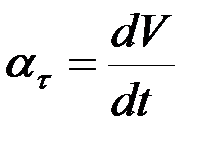 ,
, 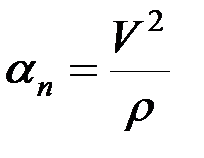 , получим
, получим 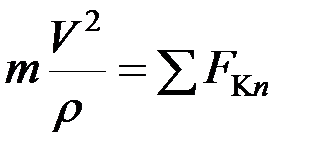 ,
, 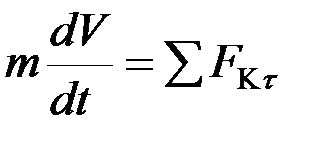 ,
, 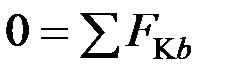 .
.
Пример. Движение материальной точки массой m с некоторого момента времени происходит по окружности радиусом r согласно уравнению S = b + 2r·ln·t (b = const). Определить модуль равнодействующей силы, приложенной к точке, как функцию времени t.
Решение:
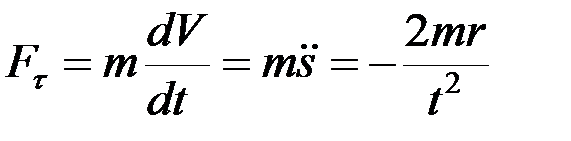 ;
; 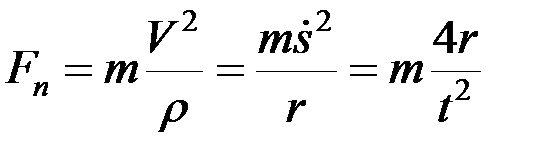 .
.
Следовательно,  .
.
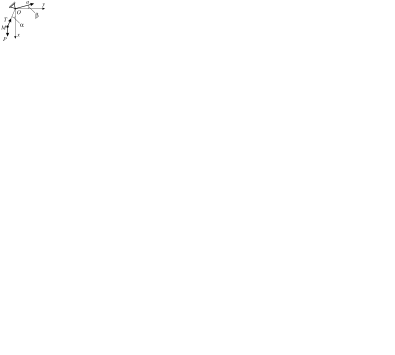 Пример. Самолет в период взлета движется поступательно и прямолинейно с постоянным ускорением а, образующим с горизонтом угол b. Определить модуль этого ускорения, если известно, что нить ОМ математического маятника, находящегося на самолете, отклонена от вертикали на угол a. Каково натяжение нити, если масса маятника равна m?
Пример. Самолет в период взлета движется поступательно и прямолинейно с постоянным ускорением а, образующим с горизонтом угол b. Определить модуль этого ускорения, если известно, что нить ОМ математического маятника, находящегося на самолете, отклонена от вертикали на угол a. Каково натяжение нити, если масса маятника равна m?
Решение:
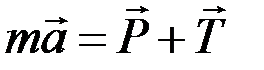 .
.
Проецируя на оси x и y, получим:
x: – mа sin b = P – T cos a, (1)
y: mа cos b = T sin a. (2)
Умножив первое уравнение на cos b, а второе – на sin b, сложив их, получим:
0 = P cos b – T cos a sin b + T sin a cos b,
откуда 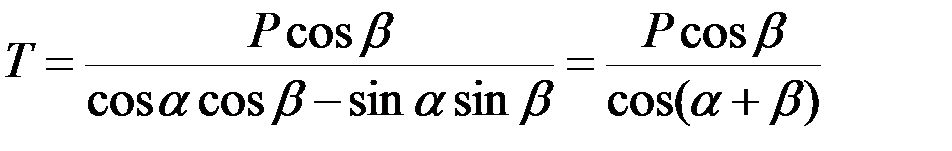 .
.
После подстановки полученного значения силы Т в уравнение (2) получим:
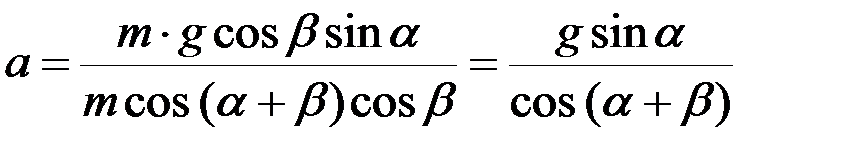 .
.
Дата добавления: 2015-08-08; просмотров: 1590;
