Анализ устойчивости по расположению корней характеристического уравнения
В разделе 2.1 отмечалось, что характер изменения функции
g(t) =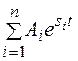 
(и её производных) зависит исключительно характера корней характеристического уравнения системы (2.17) или (2.31). Наглядное представление о характере корней и его влияния на вид функции g = g(t) даёт их расположение на комплексной плоскости. Будут рассматриваться только некратные корни поскольку в дальнейшем будет необходимо обеспечивать условия, при которых система устойчива с некотором запасом. Итак, возможны следующие варианты решения характеристического уравнения.
1. Все корни si < 0, i = 1, 2, …, n, вещественные и отрицательные, следовательно, все экспоненты импульсной переходной характеристики g = g(t) – убывающие функции времени и их сумма в пределе равна нулю.
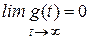. Система асимптотически устойчивая.
2. Все корни si < 0 , i = 2, 3, …, n, вещественные и отрицательные, один корень – положительный s1> 0. Эта единственная экспонента с течением времени возрастает и потому g = g(t) – возрастающая функция времени
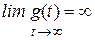. Система неустойчивая.
3. Все корни si < 0 , i = 3, 4, …, n, вещественные и отрицательные, пара комплексно – сопряженных корней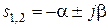 
, a > 0. При изучении импульсной переходной характеристики колебательного звена было показано, что комплексно – сопряженным корням с отрицательной вещественной частью (см. (2.50)) соответствует затухающий колебательный процесс (см. рис. 2.11). Следовательно (с учетом сказанного в пункте 1), функция g = g(t) в пределе равна нулю
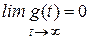. Система асимптотически устойчивая.
 |
4. Все корни si < 0 , i = 3, 4, …, n, вещественные и отрицательные, пара комплексно – сопряженных корней
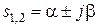, a > 0 имеет положительную вещественную часть. Этой паре корней соответствует незатухающий колебательный процесс и, следовательно, g = g(t) – возрастающая функция времени
 |
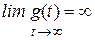. Система неустойчивая.
Из всего перечисленного вытекают следующие заключения:
· Система устойчива, если все корни её характеристического уравнения имеют отрицательные вещественные части, т.е. находятся в левой полуплоскости комплексной плоскости. Мнимая ось комплексной плоскости является границей устойчивости.
· Система неустойчива, если хотя бы один из корней характеристического уравнения имеет положительную вещественную часть.
· Система находится на апериодической границе устойчивости, если все корни её характеристического уравнения имеют отрицательные вещественные части, а один корень вещественный и равен нулю.
· Система находится на колебательной границе устойчивости, если все корни её характеристического уравнения имеют отрицательные вещественные части, а пара комплексно – сопряженных корней имеет нулевую вещественную часть.
Дата добавления: 2015-07-30; просмотров: 1480;