Критерий Михайлова
Итак, расположение корней характеристического уравнения на комплексной плоскости несёт полную информацию об устойчивости системы. Проблема заключается в том, что сложно или невозможно решить аналитически алгебраическое уравнение n – го порядка. Поэтому разработаны методы, позволяющие по косвенным признакам судить об устойчивости, не решая характеристического уравнения. Эти методы называются критериями устойчивости. Ниже будут рассмотрены два частотных критерия: критерий Михайлова и критерий Найквиста.
Пусть s1, s2,…, sn – корни характеристического уравнения системы. Из них l корней неустойчивых а оставшиеся n-l корней – устойчивых. Воспользовавшись теоремой Виета, представим характеристическое уравнение в виде
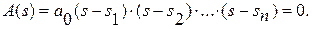(2.65)
Подставляя в уравнение (2.65) вместо текущей переменной s её значение s = jω, сформируем комплексный вектор
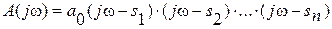(2.66)
 |
и найдем изменение фазы этого вектора DϕA при изменении частоты
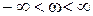. Но вектор 
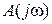представляется в (2.66) как произведение векторов разностей 
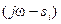, следовательно, изменение фазы DϕA равно сумме изменений фазы этих векторов разностей. Изображение векторов разностей 
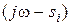на комплексной плоскости (см. рис 2.24) позволяет сделать следующее заключение:
· все устойчивые вектора разностей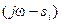 
, лежащие в левой полуплоскости, при изменении частоты ω в диапазоне 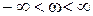поворачиваются против часовой стрелки на угол, равный 180˚,
· все неустойчивые вектора разностей 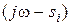, лежащие в правой полуплоскости, при изменении частоты ω в диапазоне 
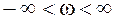поворачиваются по часовой стрелке на угол, равный -180˚.
Таким образом,
.
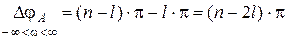Но, частотные характеристики симметричны относительно точки ω = 0. Поэтому изменение фазы вектора 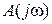, называемое действительным, определяют при изменении частоты ω в диапазоне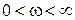 
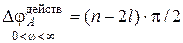. (2.67)
Если система в замкнутом состоянии устойчива (l = 0), то требуемое значение изменения фазы вектора 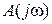равно
. (2.68)
Поскольку анализ устойчивости системы проводится в условиях, когда неизвестны значения корней характеристического уравнения, для определения 
нужно построить годограф вектора 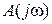, годограф Михайлова, на комплексной плоскости и по нему найти значение .
Итак,
· для того чтобы система в замкнутом состоянии была устойчивой, необходимо, чтобы
= . (2.69)
Это означает, что годограф Михайлова в положительном направлении (против часовой стрелки) должен обойти n квадрантов, т. е. повернуться на угол, равный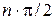 
,
· система не является устойчивой, если
< . (2.70)
т.е. нарушена последовательность обхода квадрантов,если при ω = 0 годограф Михайлова выходит из начала координат, то система находится на апериодической границе устойчивости,
· если на некоторой частоте годограф Михайлова проходит через начало координат, то система находится на колебательной границе устойчивости.
Дата добавления: 2015-07-30; просмотров: 794;