Пример 2.1

Передаточная функция системы в разомкнутом состоянии (см. рис. 2.15) имеет вид.

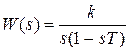. (2.74)

Требуется определить, устойчива ли система в замкнутом состоянии.

Для решения этого вопроса следует применить критерий Найквиста в следующей последовательности:

1. Определить число неустойчивых корней характеристического уравнения системы в разомкнутом состоянии.

Приравниванием нулю знаменателя передаточной функции (2.73), получаем характеристическое уравнение системы в разомкнутом состоянии и его корни

C(s) = s(1 - sT); s₁ = 0, s₂ = 1/T.

Первый корень s₁, соответствующий интегрирующему звену, является нулевым, второй – неустойчивый s₂ > 0.

Как отмечалось в разделе 2.4.6, нулевой корень s = 0 интегрирующего звена считают условно устойчивым. Таким образом, число неустойчивых корней системы в разомкнутом состоянии l_c = 1.

2. Найти требуемое значение 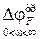вспомогательного вектора F(jω).

В соответствии с соотношением (2.71) .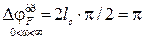

3. Построить АФХ системы в разомкнутом состоянии.

Комплексный коэффициент передачи системы в разомкнутом состоянии согласно (2.74) имеет вид

.

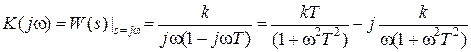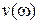В таблице 1 отражена зависимость от частоты ω значений вещественной и мнимой частей комплексного коэффициента передачи, а на рис. 2.25 изображен график АФХ, построенный по этим данным, дополненный дугой бесконечно большого радиуса поскольку передаточная функция (2.74) содержит интегрирующее звено.

Таблица 2.1

ω
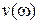
	kT	–∞
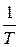
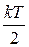
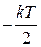
∞	+0	-0

Определение действительного значения изменения фазы 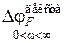вектора F(jω).

Фаза вектора F(jω), проведенного из точки (-1, 0), при изменении частоты ω от 0 до ∞ сначала уменьшается до значения, близкого -90°,а потом увеличивается до нуля. Таким образом, .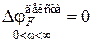

4. Заключение об устойчивости.

Поскольку в рассматриваемом случае 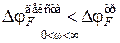, то согласно условию (2.73) система в замкнутом состоянии неустойчива.