Общий случай критерия Найквиста
Задана система с единичной отрицательной обратной связью (см. рис. 2.15) передаточной функцией в разомкнутом состоянии 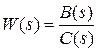 . Приравняв нулю полином знаменателя, получим характеристическое уравнение системы в разомкнутом состоянии. Пусть в общем случае lc корней этого уравнения неустойчивы, а n - lc – устойчивы. Тогда в соответствии с критерием Михайлова изменение фазы вектора C(jω) равно
. Приравняв нулю полином знаменателя, получим характеристическое уравнение системы в разомкнутом состоянии. Пусть в общем случае lc корней этого уравнения неустойчивы, а n - lc – устойчивы. Тогда в соответствии с критерием Михайлова изменение фазы вектора C(jω) равно
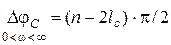 .
.
Система в замкнутом состоянии должна быть устойчивой, следовательно, должны быть устойчивыми все корни характеристического уравнения системы в замкнутом состоянии A(s) = 0 и изменение фазы вектора A(jω) равно
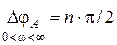 .
.
Вводится вспомогательная переменная F(s). В соответствии с формулой (2.61), она равна отношению характеристических полиномов системы в замкнутом и разомкнутом состояниях
F(s) = 1 + W(s) = 1 + 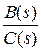 =
= 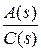 . (2.70)
. (2.70)
Применение критерия Михайлова позволяет определить изменение фазы вектора F(jω)
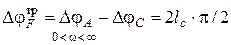 .
.
Таким образом,
· для того, чтобы система в замкнутом состоянии была устойчивой, необходимо, чтобы
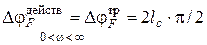 ,
,
· система в замкнутом состоянии неустойчива, если
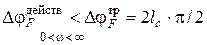 .
.
Дата добавления: 2015-07-30; просмотров: 814;
