Вероятность попадания двумерной случайной величины в полуполосу и прямоугольник.
Вероятность попадания двумерной случайной величины в прямоугольник определяется, исходя из определения интегральной функции двумерной случайной величины (рис.1):
P ((x, y)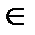 
D) = F (b,d) - F (a,d) - F (b, 
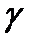) + F (a, 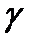) (6.5)
| d |
| g |
| a |
| b |
| D |
| y |
| x |
Рис. 1. Вероятность попадания точки (х, y) в прямоугольник D
Случайные величины X, Y независимы, если F(x, y) = F1(x) F2(y).
Дата добавления: 2015-08-11; просмотров: 1534;