Неравенство и теорема Чебышева

Лемма Чебышева (Маркова). Если случайная величина X принимает только неотрицательные значения и имеет математическое ожидание M(X), то для любого 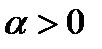имеет место неравенство:

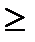
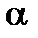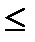
P(X ) 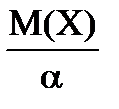. (7.1)

Неравенство Чебышева. Если случайная величина Х имеет математическое ожидание M(X) и дисперсию D(X), то для любого 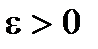имеет место неравенство:

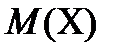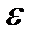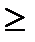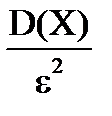P(|x- |< ) 1- . (7.2)

Неравенство Чебышева является в теории вероятностей общим фактом и позволяет оценить нижнюю границу вероятности.

Если произведено n независимых испытаний по схеме Бернулли, где p – вероятность успеха, q - вероятность неудачи, n - число опытов, к - число успехов, то для случайной величины имеет место неравенство:

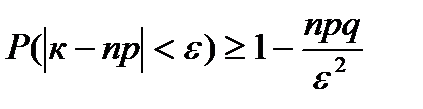. (7.3)

Для относительной частоты появления события 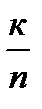аналогичное неравенство имеет вид:

. (7.4)

Теорема. Закон больших чисел Чебышева. Пусть X₁, X₂, …,X_n - последовательность попарно независимых случайных величин, имеющих конечные математические ожидания и дисперсии, ограниченные сверху постоянной С = const (D(X_i) 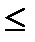С (i=1, 2,…,n)). Тогда для любого 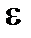>0,

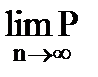
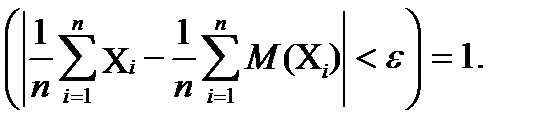(7.5)

Теорема показывает, что среднее арифметическое большого числа случайных величин с вероятностью, сколь угодно близкой к 1, будет мало отклоняться от среднего арифметического математических ожиданий.

Следствие 1. Если вероятность наступления события A в каждом из n независимых испытаний равна p, к - число наступлений события A в серии из n независимых испытаний, то, каково бы ни было число 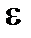>0, имеет место предел:

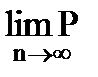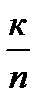(| -p|< 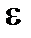) = 1 (7.6)

Таким образом устанавливается связь между относительной частотой появления события A и постоянной вероятностью р в серии из n независимых испытаний.

Следствие 2. Теорема Пуассона. Если в последовательности независимых испытаний вероятность появления события А в r-ом испытании равна р_r, то

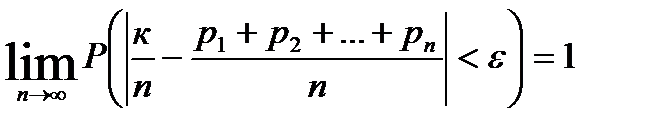(7.7)

где к - число появлений события А в серии из n испытаний.

Следствие 3. Теорема Бернулли. Если X₁, X₂, …,X_n - последовательность независимых случайных величин таких, что M(X₁) = M(X₂) =…= M(X_n) = а, D(X₁) < C, D(X₂) < C,…,D(X_n) < C, где C = const, то, каково бы ни было постоянное число 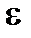>0, имеет место предел:

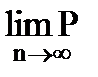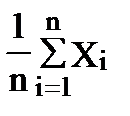(| -а|< 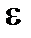) = 1. (7.8)

Законы больших чисел не позволяют уменьшить неопределённость в каждом конкретном случае, они утверждают лишь о существовании закономерности при достаточно большом числе опытов. Например, если при подбрасывании монеты 10 раз появился герб, то это не означает, что в 11 раз появится цифра.