Понятие о центральной предельной теореме

В теории вероятностей и математической статистике большое значение имеет центральная предельная теорема Ляпунова, в которой утверждается, что если сложить большое число случайных величин, имеющих один или различные законы распределения, то случайная величина, являющаяся результатом суммы, при некоторых условиях будет иметь нормальный закон распределения.

Примером центральной предельной теоремы (для последовательности независимых случайных величин) является интегральная теорема Муавра-Лапласа.

Теорема 1. Пусть производится n независимых опытов в каждом из которых вероятность наступления события А равна р (не наступления q=1-р, p¹0, p¹1). Если К - число появлений события А в серии из n испытаний, то при достаточно больших n случайную величину К можно считать нормально распределенной (M(К)=np, ):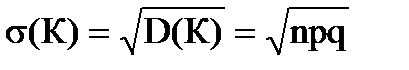

P(К<к) 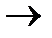P(X<x₀) = 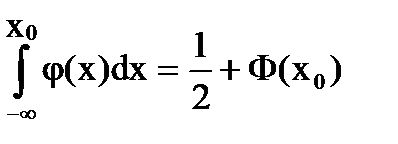, (7.9)

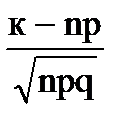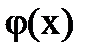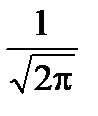
где x_{0 =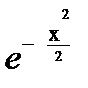} , = , Ф(x₀) - функция Лапласа.

В более общем случае верна следующая теорема.

Теорема 2. Если случайные величины Х₁, Х₂,… Х_n независимы, одинаково распределены и имеют конечную дисперсию, то при n®¥:

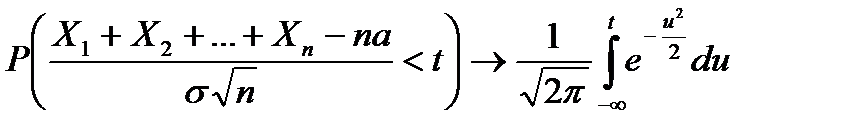, (7.10)

где M(Х_i)=а, s²=D(Х_i);

U - нормально распределенная случайная величина, M(U)=0, D(U)=1.