Понятие и виды вариационных рядов распределения
В реальных социально - экономических системах нельзя проводить активные эксперименты, поэтому данные обычно представляют собой наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений − это, в общем случае, ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжировать).
Операция, заключенная в расположении значений признака по возрастанию, называется ранжированием данных.
После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (Xi). Значит вариант – это значение признака у единицы совокупности, отличное от значений его у других единиц. Число элементов в каждой группе называется частотой варианта (ni).
Размахом вариации называется число W=xmax-xmin, где
xmax- наибольший вариант, xmin- наименьший вариант.
Сумма всех частот равна определенному числу n, которое называется объемом совокупности:
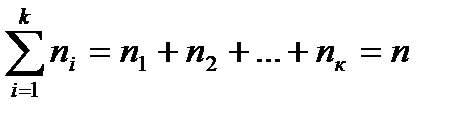 . (9.1)
. (9.1)
Отношение частоты данного варианта к объему совокупности называется относительной частотой ( 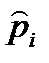 ) или частостью этого варианта:
) или частостью этого варианта:
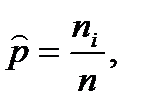 (9.2)
(9.2)
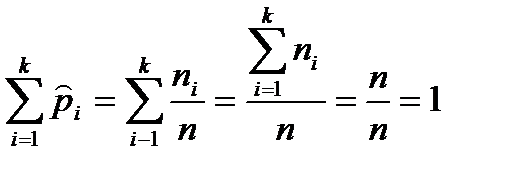 . (9.3)
. (9.3)
Последовательность вариант, расположенных в возрастающем порядке, с соответствующими им частотами или частостями называется вариационным рядом (вариация - изменение).
Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.
Дата добавления: 2015-08-11; просмотров: 1151;
