Числовые характеристики системы двух случайных величин
Начальным моментом порядка s,h системы двух случайных величин X, Y называется математическое ожидание произведения степени s случайной величины Х и степени h случайной величины Y:
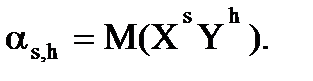 (6.6)
(6.6)
Центральным моментом порядка s, h систем двух случайных величин (X, Y) называется математическое ожидание произведения степеней s, h соответствующих центрированных случайных величин
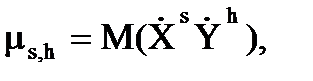 (6.7)
(6.7)
где 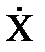 = X – M (X),
= X – M (X), 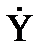 = Y - M (Y)-центрированные случайные величины X и Y.
= Y - M (Y)-центрированные случайные величины X и Y.
Основным моментом порядка s, h систем двух случайных величин (X,Y) называется нормированный центральный момент порядка s, 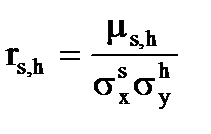 . (6.8)
. (6.8)
Начальные моменты a1,0, a0,1:
a1,0 = M ( 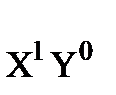 )= M (X); a0,1 = M (
)= M (X); a0,1 = M ( 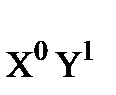 ) = M (Y). (6.10)
) = M (Y). (6.10)
Вторые центральные моменты:
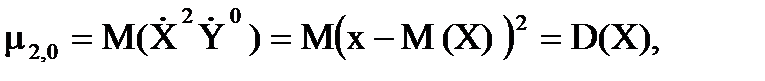
Характеризует рассеяние случайных величин в направлении оси 0X.
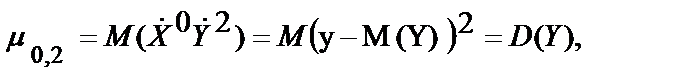 (6.11)
(6.11)
Характеризует рассеяние случайных величин в направлении оси 0Y.
Особую роль в качестве характеристики совместной вариации случайных величин X и Y играет второй смешанный центральный момент, который называется корреляционным моментом (ковариацией):
μ1,1=M( 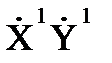 )=К(X,Y)=cov(X, Y)=M(XY) - M(X)M(Y). (6.12)
)=К(X,Y)=cov(X, Y)=M(XY) - M(X)M(Y). (6.12)
Корреляционный момент является мерой связи случайных величин.
Если случайные величины X и Y независимы, то математическое ожидание ХУ равно произведению их математических ожиданий:
M (XY)= M (X) M (Y), отсюда cov (X,Y)=0.
Если ковариация случайных величин не равна нулю, то случайные величины коррелированны. Ковариация может принимать значения на всей числовой оси, поэтому в качестве меры связи используют основной момент порядка s=1, h=1,который называют коэффициентом корреляции:
rxy= 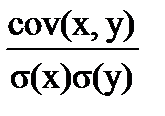 , (6.13)
, (6.13)
где 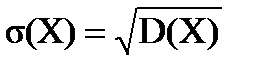 ,
, 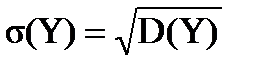 .
.
Коэффициент корреляции служит мерой линейной зависимости между случайными величинами.
Свойства коэффициента корреляции:
1. -1 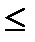 rxy
rxy 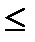 1;
1;
2. Если rxy = 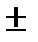 1, то случайные величины линейно зависимы;
1, то случайные величины линейно зависимы;
3. Если rxy = 0, то случайные величины не коррелированны, что не означает их независимости вообще.
Замечание. Если случайные величины Х и Y подчиняются нормальному закону распределения, то некоррелированность СВ Х и Y означает их независимость.
Первые моменты:
а) для дискретных СВ: б) для непрерывных СВ:
M (X)= 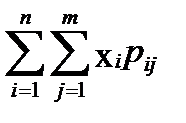 ,
M(Y)= ,
M(Y)= 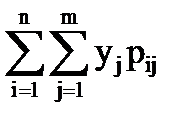 , D(X)= , D(X)= 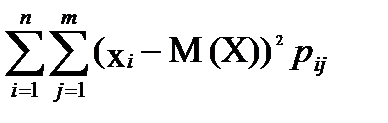 ,
D(Y)= ,
D(Y)= 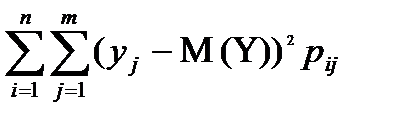 ,
K(X,Y)= ,
K(X,Y)= 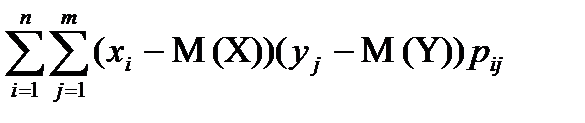 ; ;
| M(X)= 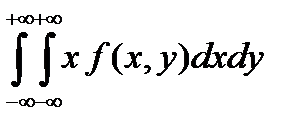 , M(Y)= , M(Y)= 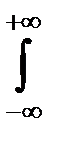 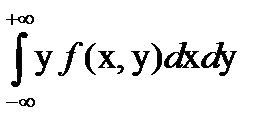 ,
D(X)= ,
D(X)= 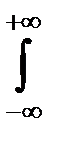 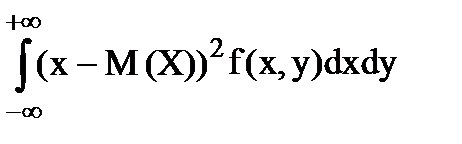 ,
D(X)= ,
D(X)= 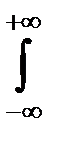 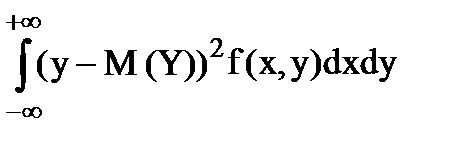 ,
K(X,Y)= ,
K(X,Y)= 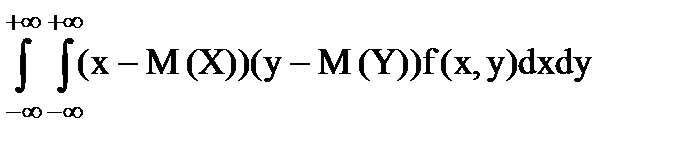 . .
|
Дата добавления: 2015-08-11; просмотров: 892;
