Функции распределения многомерной случайной величины.

В общем случае двумерная случайная величина задается в виде интегральной функции: F(x, y) = P(X<x, Y<y), которая означает вероятность попадания двумерной случайной величины в квадрант левее и ниже точки с координатами (x, y).

Свойства интегральной функции:

1. F- не убывающая и непрерывная функция слева по каждому аргументу;

2. F(- 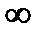, y)= F(x,- 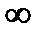)= F(- 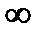, - 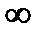)= 0;

3. F(+ 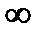, y)= F₂(y) – функция распределения случайной величины Y;

F(x,+ 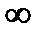)= F₁(x) – функция распределения случайной величины X;

4. F(+ 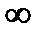, + 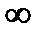)= 1.

Дифференциальная функция системы двух непрерывных случайных величин определяется как вторая смешанная производная функции распределения:

f (x, y) = 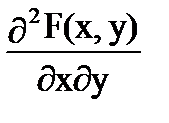= 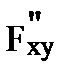(x, y). (6.1)

Свойства дифференциальной функции:

1.f (x, y)>0;

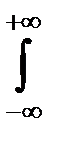
2. 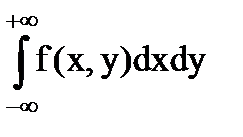= 1;

3.F(x, y) = .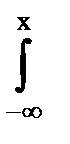

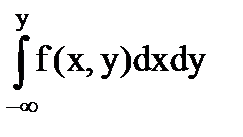Геометрически свойство 2 означает, что объем тела ограниченного поверхностью f (x, y) и плоскостью XОY равен 1.

Если случайные величины x и y независимы, то

f(x, y) = f₁(x) f₂(y), (6.2)

где f₁(x)= 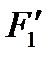(x), f₂(y)= 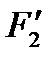(y) − безусловные законы распределения.

В противном случае:

f(x, y) = f₁(x) f(y/x) или f(x,y) = f₂(y) f(x/y), где

f(y/x)= - (6.3)

условная дифференциальная функция случайной величины Y при заданном значении X = x,

f(x/y)= 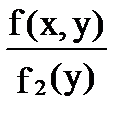- (6.4)

условная дифференциальная функция случайной величины X при заданном значении Y= y;

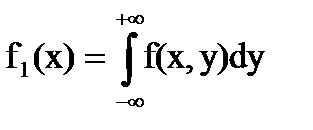и 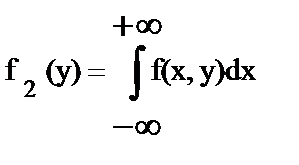- дифференциальные функции отдельных величин X и Y, входящих в систему.