Композиция законов распределения

В приложениях часто рассматривается вопрос о распределении суммы нескольких случайных величин. Например, пусть Z=X+Y, тогда G(z) -интегральную функцию случайной величины Z можно определить по формуле:

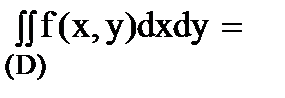
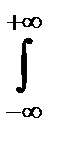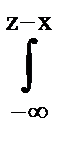G(z) = dy f(x, z-x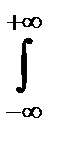)dx= dx f(z-y,y)dy, (5.4)

где f(x,y)-дифференциальная функция системы случайных величин (X,Y);

область D – полуплоскость, ограниченная сверху прямой y=z-x.

Отсюда, .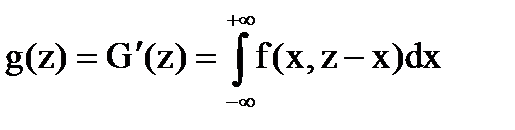

Если X и Y независимы, то говорят о композиции законов распределения случайных величин и дифференциальная функция случайной величины Z определяется как

g(z)= 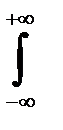f ₁ (x) f₂(z-x)dx= 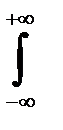f ₁ (z-y) f₂(y)dx, (5.5)

где f ₁ (x) и f₂(y) дифференциальные функции случайной величины X и Y соответственно.

Если возможные значения аргументов неотрицательны, то дифференциальную функцию случайной величины Z определяют по формуле:

g(z)= 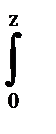f ₁ (x) f₂(z-x)dx (5.6)

или

g(z)= 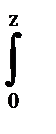f ₁ (z-y) f₂(y)dy. (5.7)