Виды статистических оценок параметров распределения

Все статистические оценки подразделяют на точечные и интервальные.

Статистика, используемая в качестве приближенного значения неизвестного параметра генеральной совокупности, называется ее точечной оценкой. Таким образом, точечная оценка определяется одним числом.

Если рассматривают выборку малого объема, то точечная оценка

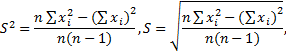
может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

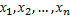Выборочной средней называют среднее арифметическое значение признака выборочной совокупности. Если все значения признака выборки объема n различны, то находится по формуле

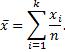
Если значения признака 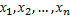имеют соответствующие частоты, то среднюю выборочную рассчитывают следующим образом

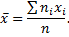
Таким образом, выборочная средняя, найденная по данным одной выборки, есть конкретное число.

Если извлекать другие выборки того же объема из одной генеральной совокупности, то выборочная средняя будет изменяться от выборки к выборке.

Вывод: выборочную среднюю можно рассматривать как случайную величину, т.е. можно говорить о распределениях (теоретическом и эмпирическом) выборочной средней и о числовых характеристиках этого распределения.

Отклонением от общей средней называют разность 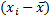между значением признака и общей средней. Сумма произведений отклонений на соответствующие частоты равна нулю

.

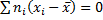Выборочной дисперсией 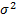называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения . Если значения признака 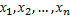имеют соответственно частоты и , то выборочная дисперсия рассчитывается по формуле

Кроме дисперсии для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения используют еще одну характеристику – среднее квадратическое отклонение. Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии

Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности. Среднее квадратическое отклонение показывает, насколько в среднем отклоняются конкретные варианты от их среднего значения.

По вышеуказанным данным выборки, возможно, оценить неизвестные генеральную дисперсию и генеральное среднее квадратическое отклонение. Для этого используют несмещенную оценку генеральной совокупности – исправленную дисперсию

Для оценки среднеквадратического отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое не является несмещенной оценкой

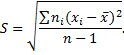
Коэффициент вариации представляет собой выраженное в процентах отношение среднеквадратического отклонения к средней арифметической

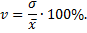
Коэффициент вариации используют для сравнительной оценки вариации единиц совокупности и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает .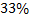

Кроме перечисленных выше характеристик вариационного ряда используют и другие, такие как мода 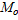, медиана 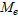, среднее абсолютное отклонение .

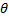Модой 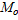называют варианту, которая имеет наибольшую частоту.

Медианой 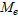называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. n=2k+1, то 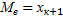; если число вариант четно, т.е. n=2k, то

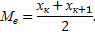
Например, для ряда 2 3 5 6 7 медиана равна 5; для ряда 2 3 5 6 7 9 медиана равна

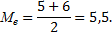
Средним абсолютным отклонением 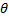называют среднее арифметическое абсолютных отклонений

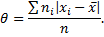
Среднее абсолютное отклонение служит для характеристики рассеяния вариационного ряда.

Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.