Эмпирическая функция распределения
Статистическое распределение можно задавать в виде последовательности интервалов и соответствующих им частот.
Если в основании группировки лежит качественный признак, то количество групп равняется количеству значений этого признака. Если в основании группировки лежит количественный признак, то число групп и величина равных интервалов определяется по формуле Стерджеса
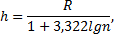
где R – размах выборки, n – объем выборки. Размах выборки равен разности между наибольшим и наименьшим значением наблюдаемых вариант выборки
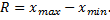
Частота, соответствующая интервалу, принимает значение, равное сумме частот, попавших в этот интервал.
Введем обозначения: 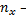 число наблюдений, при которых наблюдалось значение признака, меньшее
число наблюдений, при которых наблюдалось значение признака, меньшее  ; n – общее число наблюдений (объем выборки).
; n – общее число наблюдений (объем выборки).
Относительная частота события 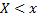 будет равна
будет равна 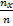 . Если изменяется
. Если изменяется  , то изменяется и относительная частота, т.е. относительная частота
, то изменяется и относительная частота, т.е. относительная частота 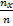 – функция от х. Так как эта функция находится опытным (эмпирическим) путем, то ее называют эмпирической
– функция от х. Так как эта функция находится опытным (эмпирическим) путем, то ее называют эмпирической

Чтобы найти, например, 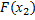 надо число вариант, меньших
надо число вариант, меньших 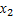 , разделить на объем выборки
, разделить на объем выборки

В отличие от эмпирической функции распределения выборки функцию распределения генеральной совокупности 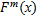 называют теоретической функцией распределения.
называют теоретической функцией распределения.
Теоретической функцией распределения называют функцию, определяющую вероятность того, что случайная величина 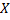 в результате испытания примет значение, меньшее
в результате испытания примет значение, меньшее  , т.е.
, т.е.
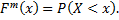
Различие между теоретической и эмпирической функциями распределения состоит в том, что теоретическая функция распределения 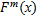 определяет вероятность события Х<x, а эмпирическая функция распределения
определяет вероятность события Х<x, а эмпирическая функция распределения 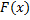 определяет относительную частоту этого же события.
определяет относительную частоту этого же события.
Согласно теоремы Бернулли, относительная частота события Х<x (т.е. 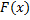 мало отличается от вероятности
мало отличается от вероятности 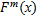 этого события при больших n). Другими словами, при больших n числа
этого события при больших n). Другими словами, при больших n числа 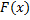 и
и 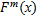 мало отличаются одно от другого в том смысле, что
мало отличаются одно от другого в том смысле, что
 .
.
Вывод: целесообразно использовать эмпирическую функцию распределения 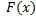 выборки для приближенного представления теоретической функции распределения
выборки для приближенного представления теоретической функции распределения 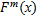 генеральной совокупности.
генеральной совокупности.
Такой вывод подтверждается тем, что 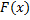 обладает всеми свойствами
обладает всеми свойствами 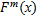 . Действительно, из определения эмпирической функции распределения вытекают следующие ее свойства:
. Действительно, из определения эмпирической функции распределения вытекают следующие ее свойства:
1) значение эмпирической функции принадлежат отрезку 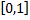 ;
;
2) 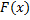 – неубывающая функция;
– неубывающая функция;
3) если 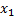 – наименьшая варианта, то
– наименьшая варианта, то 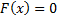 при
при  ; если
; если 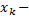 наибольшая варианта, то
наибольшая варианта, то 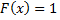 при
при 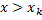 .
.
Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
Рассмотрим пример. Записать эмпирическую функцию распределения по данному распределению выборки
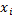
| |||

|
Решение: 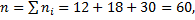
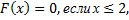
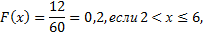
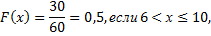
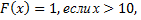
т.е.
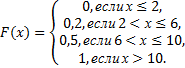
Дата добавления: 2015-08-11; просмотров: 1388;
