Генеральная и выборочная совокупности

Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей.

Предметом математической статистики является изучение случайных величин по результатам наблюдений. Полученные в результате наблюдения (опыта, эксперимента) данные сначала обрабатываются, т.е. представляют в удобном для обозрения и анализа виде. В этом первая задача. Вторая задача: оценить интересующие исследователя характеристики наблюдаемой случайной величины. Третьей задачей является проверка статистических гипотез, т.е. решение вопроса согласования результатов оценивания с опытными данными.

Результаты исследования статистических данных методами математической статистики используются для принятия решения в задачах планирования, прогнозирования, управления, организации производства, при контроле качества продукции, при выборе оптимального времени настройки или замены действующей аппаратуры и т.д., т.е. для научных и практических выводов. При большом числе наблюдений случайные воздействия в значительной мере погашаются, и получаемый результат оказывается практически неслучайным, предсказуемым. Это утверждение является основой для практического использования математико-статистических методов исследования. Цель указанных методов состоит в том, чтобы минуя сложное исследование отдельного случайного явления, изучить закономерности массовых случайных явлений, прогнозировать их характеристики, влиять на ход этих явлений, контролировать их, ограничивать область действия случайности.

Математическая статистика как наука начинается с работ немецкого математика Карла Фридриха Гаусса (1777 – 1855), который на основе теории вероятностей исследовал и обосновал метод наименьших квадратов, созданный им в 1795 г. и примененный для обработки астрономических данных. Его именем называют одно из наиболее распространенных распределений вероятностей – нормальное.

В конце девятнадцатого века крупный вклад в математическую статистику внесли английские исследователи – К. Пирсон (1857-1936) и Р. Фишер (1890-1962). Пирсон разработал критерий «хи-квадрат» проверки статистических гипотез, а Фишер – дисперсионный анализ, теорию планирования эксперимента, метод максимального правдоподобия оценки параметров.

В 30-е годы двадцатого столетия поляк Е.Нейман (1894-1977) и англичанин Э.Пирсон развили общую теорию проверки статистических гипотез, а советские математики академик А. Н. Колмогоров и член-корреспондент Н.В. Смирнов заложили основы непараметрической статистики.

Математическая статистика развивается и в настоящее время. Можно выделить четыре направления исследования:

- разработку и внедрение математических методов планирования эксперимента;

- развитие статистики объектов нечисловой природы как самостоятельного направления;

- развитие статистических методов, устойчивых по отношению к малым отклонениям от используемой вероятностной модели;

- создание компьютерных пакетов программ, предназначенных для проведения статистического анализа данных.

Часто требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака. Например, в партии деталей качественным признаком может служить стандартность детали, а количественным – контролируемый размер детали.

Выборочной совокупностью (выборкой) называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.

Например, если из 1000 деталей для обследования выбирают 100 деталей, то объем генеральной совокупности N=1000, а объем выборки n=100.

Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли, т.е. выборка должна быть репрезентативной (представительной). В силу закона больших чисел можно сказать, что выборка будет репрезентативной, если ее осуществить случайно из генеральной совокупности, т.е. если все объекты имеют одинаковую вероятность попасть в выборку.

Например, для того, чтобы оценить будущий урожай, можно сделать выборку из генеральной совокупности еще не созревших плодов и исследовать их характеристики. Если вся выборка будет сделана с одного дерева, то она не будет репрезентативной. Репрезентативная выборка должна состоять из случайно выбранных плодов со случайно выбранных деревьев.

Исследуемая статистическая совокупность в оптимальном варианте должна иметь от 30 до 200 данных. Большее число данных требует больших усилий при их обработке, меньшее их число не всегда дает достоверные результаты для анализа.

При испытаниях статистические данные поступают в произвольном, случайном порядке. Возникает необходимость эти данные систематизировать, обработать и получить результаты, которые можно анализировать.

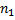Пусть из генеральной совокупности извлечена выборка, причем наблюдалось раз, 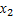– наблюдалось 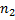раз, …, 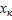– наблюдалось 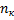раз и – объем выборки.

Значения 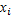называют вариантами. Последовательность вариант в возрастающем порядке называют вариационным рядом.

Числа наблюдений называют частотами, а их отношения к объему выборки

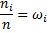
– относительными частотами.