Анализ взаимосвязи между параметрами статистической совокупности
Функциональная зависимость: при изменении одного параметра на определенную величину всегда происходит изменение другого также на определенную фиксированную величину.
Корреляционная связь: определенному значению одного параметра может отвечать несколько значений другого.
В медико-биологических исследованиях зависимость между отдельными параметрами не является функциональной связью. При изменении одного признака невозможно абсолютно точно спрогнозировать величину, на которую изменяются другие.
Определение характера связи между определенными параметрами проводят путем расчета коэффициента корреляции.
| Направленность связи – определяется по знаку коэффициента корреляции. | |||
| Прямая связь – динамика параметров однонаправленная – увеличение одного параметра обуславливает увеличение другого. | Обратная –динамика параметров разнонаправлена – увеличение одного параметра обуславливает уменьшение другого. | ||
| Сила связи | |||
| Слабая r=0.01-0.29 | Средняя r=0.30-0.69 | Сильная r=0.70-0.99 | |
Коэффициент парной корреляции отображает характер связи 2 признаков.
Он дает характеристику обобщенной «неочищенной» связи между параметрами. Он может быть рассчитан при сопоставлении двух рядов в виде
· рангового коэффициента корреляции (ρ) и
· линейного коэффициента корреляции (r).
Корреляционная зависимость различается по направлению, силе и форме связи.
По направлению корреляционная связь может быть положительной ("прямой") и отрицательной ("обратной"). Степень, сила или теснота корреляционной связи определяется по величине коэффициента корреляции. Сила связи не зависит от ее направленности и определяется по абсолютному значению коэффициента корреляции.Максимальное возможное абсолютное значение коэффициента корреляции r = 1,00; минимальное r = 0,00.
Коэффициент ранговой корреляции (Спирмена) - непараметрический метод, который используется с целью статистического изучения связи между явлениями.
Особенность коэффициента Спирмена – простота вычисления при недостаточной точности позволяет его использовать для ориентировочного анализа с проведением быстрых расчетов, при определении данных в получисленном описательном виде.
Этапы расчета:
1) Определить ранги значения каждой величины рядов X и Y.
Ранжирование обоих рядов должно быть однонаправленным.
2) Определить отклонение значений одного ряда от другого (dxy).
Их сумма с учетом знаков должна равняться 0.
3) Возвести полученные результаты в квадрат, и определить их сумму
( 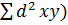
4) Подставляем полученные результаты в формулу:
ρ =1- 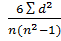
где  - сумма квадратов разностей рангов, а
- сумма квадратов разностей рангов, а  - число парных наблюдений.
- число парных наблюдений.
Для оценки достоверности коэффициент корреляции должен превышать свою погрешность не меньше, чем в 2,5 – 3 раза при достаточном числе наблюдений.
При большом числе наблюдений (n˃100) средняя ошибка рангового коэффициента корреляции вычисляется по формуле:
mρ 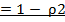
√n
Оценка достоверности коэффициента корелляции проводится по тем же принципам, что используются для других показателей с определением числа наблюдений (числа степеней свободы вариационных рядов n'=n-2. Полученные результаты сравнивают с табличными значениями для соответствующих ступеней вероятности ошибки первого типа.
Линейный коэффициент корелляции Пирсона:
r=Ʃdx х dy
√Ʃdx2 x Ʃdy2
где X и Y – варианты сравниваемых вариационных рядов
dx и dy – отклонения каждой варианты от своей средней арифметической
Расчет линейного коэффициента корреляции:
1.Определяют средние значения для каждого ряда (Хх, Ху).
2. Определяют отклонение каждого из значений ряда от средней
величины (dх, dу).
3. Возводят определенные отклонения в квадрат и определяют их
суммы: 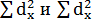
Достоверность полученного результата определим по соотношению
t = r / mr, где mr при малом числе наблюдений (n < 30) равняется:
mr= 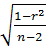
При большом числе наблюдений (n > 100):
m= 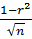
Прямолинейная корреляционная связь между параметрами:
каждому из одинаковых измерений одного показателя отвечает определенное среднее значение другого показателя. Данную зависимость можно описать коэффициентом регрессии. Рассчет коэффициент регрессии:
Rx/y=rxy* 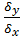
Где: Rx/y - коэффициент регрессии от Х до У;
rxy - коэффициент корреляции;
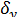 и
и 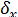 средние квадратические отклонения рядов Х и У.
средние квадратические отклонения рядов Х и У.
Коэффициенты регрессии широко используются для построения уравнений регрессии при разработке многих медико-социальных и клинических проблем. Данные уравнения — математическая модель, которая описывает характер взаимосвязи между исследуемыми параметрами. Коэффициент регрессии показывает, на какую величину в среднем изменится второй параметр при изменении первого на определенную единицу измерения.
Дата добавления: 2015-08-04; просмотров: 2988;
