Алгоритм
1. Составить список испытуемых в любом порядке, например, алфавитном.
2. Вычислить разность между индивидуальными значениями во втором и первом замерах. Определить, что будет считаться типичным сдвигом.
3. Согласно алгоритму ранжирования, проранжировать абсолютные величины разностей, начисляя меньшему значению меньший ранг, и проверить совпадение полученной суммы рангов с расчетной.
4. Отметить каким-либо способом ранги, соответствующие сдвигам в нетипичном направлении. Подсчитать их сумму Т.
5. Определить критические значения Т для данного объема выборки. Если Т-эмп. меньше или равен Т-кр. – сдвиг в «типичную» сторону достоверно преобладает.
Фактически оцениваются знаки значений, полученных вычитанием ряда значений одного измерения из другого. Если в результате количество снизившихся значений примерно равно количеству увеличившихся, то гипотеза о нулевой медиане подтверждается.
Различия между независимыми группами. Если имеются две выборки (например, мужчины и женщины), которые нужно сравнить относительно некоторого среднего значения, например, среднего давления или количества лейкоцитов в крови, то можно использовать t-тест для независимых выборок.
Непараметрической альтернативой этому тесту является двухвыборочный критерий Колмогорова— Смирнова.
Критерий согласия Колмогорова-Смирнова(λ2) и критерий согласия Пирсона (χ2) применяют в случае сравнения независимых друг от друга совокупностей (сравнение опытной и контрольной групп больных, результатов двух групп наблюдений с разными заболеваниями или степенями тяжести патологии).
Методика расчета критерия Колмогорова – Смирнова (λ2):
1.Числовые значения двух вариационных рядов объединяют в один вариационный ряд, варианты какого упорядочивают в порядке роста.
2.Определяют частоты вариант для обеих групп наблюдений|.
3.Определяют накопленные частоты для обеих групп.
4.Определяют накопленные частицы|долю|, для чего накопленные частоты делятся|делящийся| на число наблюдений для каждой группы.
5.Рассчитывается разница|разность| накопленных частиц|доли| групп X и У без учета знаков.
6.Определяют максимальную разницу|разность|
7.Определяют критерий 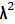
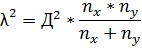
8.Сравнивают полученный результат с предельным значением критерия
Колмогорова-Смирнова|.
Если 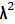 больше предельного значения, разница между сравниваемыми группами является существенной.
больше предельного значения, разница между сравниваемыми группами является существенной.
При проведении статистического анализа иногда необходимо оценить достоверность разницы более двух показателей клинико-статистических групп.
В указанных ситуациях наиболее целесообразным является использование критерия согласия χ2 (критерий Пирсона):χ2= 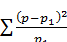
где p - истинные частоты
p1 - теоретические частоты
Практическое значение критерия соответствия χ2:
• оценивание достоверности разницы|разности| между несколькими сравниваемыми группами при нескольких возможных результатах с разной|различной| степенью вероятности (например, три или четыре группы больных с разными|различными| методами лечения и их последствиями — разной|различной| частотою| осложнений|усложнения|);
• определение наличия связи между двумя факторами (зависимость результатов лечения от возраста|века| больных, тяжести заболевания, связь между тяжестью патологии новорожденных и состоянием|станом| их физического развития);
• оценивание идентичности распределения|деления| частот в двух и более совокупностях (аналогичность распределения|деления| больных по уровню клинических параметров при разных|различных| степенях тяжести патологии).
Основой метода является определение существенности разницы (отклонений) фактических данных от теоретических (ожидаемых). Расчет теоретических данных базируется на предположении, что между сравниваемыми группами по исследуемым факторам разницы нет. Данное предположение определяется как «нулевая» гипотеза.
На основе «нулевой» гипотезы определяют «ожидаемые|» результаты и сравнивают их с фактическими данными. Если разницы|разности| нет, можно сделать|совершить| вывод, что «нулевая» гипотеза подтвердилась. При наличии отличий фактических данных от теоретического расчета | определяют существенность разницы|разности| между сравниваемыми| группами.
Оценивание результатов (χ2) проводится по специальной таблице. Существенной считается разница в том случае, когда величина рассчитанного коэффициента превышает табличное значение при достоверности не ниже 95% (вероятность погрешности менее 5%-р<0,05).
Методика расчета коэффициента согласия χ2:
1.Приведем фактические результаты по трём методам| лечения
| Методика лечения | Всего больных | Результаты лечения – Р (фактические данные) | ||
| хорошо | удовлетворительно | неудовлетворительно | ||
| I | ||||
| II | ||||
| III | ||||
| Всего | 200 (100%) |
2.Рассчитываем «ожидаемые» результаты согласно «нулевой» гипотезе, основой|основанием| которой|какой| является доказательство, что разницы|разности| между результатами лечения по отдельным методикам нет. В этом случае за основу|основание| берем общее деление|разделение| больных, вылеченных всеми методами. Числовая характеристика «нулевой» гипотезы составляет: хорошие результаты в целом имели 54,5 %, удовлетворительные — 26,5 % | и неудовлетворительные — 19 % больных. В соответствии с|соответственно| указанным делением|разделением| определяем «ожидаемые» данные результатов лечения по отдельным методикам (значение определяем в целых числах)
| Методика лечения | Всего больных | Результаты лечения – Р1 (ожидаемые данные) | ||
| хорошо | удовлетворительно | неудовлетворительно | ||
| I | ||||
| II | ||||
| III | ||||
| Всего | 200(100%) | 109 (54,5%) | 53 (26,5%) | 38 (19%) |
3.Сопоставляем фактические и теоретические данные (их разницу|) с расчетом величины отклонения и учетом| его направления (знака)
| Методика лечения | ( Р - Р1 ) | ||
| хорошо | удовлетворительно | неудовлетворительно | |
| I | 9 (36-27) | -2 (11-13) | -7 (3-10) |
| II | 4 (48-44) | -4 (17-21) | 0 (15-15) |
| III | -13 (25-38) | 6 (25-19) | 7 (20-13) |
| Всего |
4.Рассчитываем квадрат отклонения теоретических данных от фактических и средний квадрат отклонения на одну «ожидаемую» группу. Данный этап расчета имеет такой вид в связи с тем, что на основе фактических отклонений невозможно определить его суммарную величину, поскольку она равняется нулю. При возведении отклонений в квадрат определяем их параметры для каждой группы (р — р1)2. Учитывая разное число больных в исследуемых группах величина отклонений может быть разной, потому квадрат их делим на число соответствующих наблюдений каждой группы — (р — р1)2 / р1. Проведя расчеты, определяем (р — р1)2 и (р — р1)2 / р1.
| Методика лечения | ( Р - Р1 ) 2 | ( Р - Р1 ) 2 / Р1 | ||||
| хорошо | удовлетворительно | неудовлетворительно | хорошо | удовлетворительно | неудовлетворительно | |
| I | 0,3 | 4,9 | ||||
| II | 0,4 | 0,8 | ||||
| III | 4,4 | 1,9 | 3,8 | |||
| Σ=19,5 |
5.Определяем χ2— итог результатов последнего этапа расчетов. В нашем случае χ2= 19,5.
Сравниваем его с табличным значением, учитывая число степеней свободы (n1), которые определяют по формуле: n1= (S-| 1) (г-| 1),
где S — число групп больных (для нашего примера |приклада| - три).
г — число результативных групп (три).
|Число степеней свободы n1= (3 - 1) (3 - 1) = 4.
Полученный результат превышает табличное значение χ2для n1 = 4 по всем уровням достоверности. Следовательно, мы можем сделать вывод о существенности (достоверности) разницы между показателями при разных методах лечения — «нулевая» гипотеза не подтвердилась.
Дата добавления: 2015-08-04; просмотров: 1519;
