Ақиқаттық кесте бойынша МКҚФ құрудың алгоритмі.

Алгоритмді f (x1 ,x2,x3 ) = 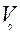(0,3,7) функциясына МКҚФ құруға қолданайық.

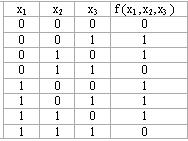
1. Кестеден функцияны 0-ге айналдыратын аргументтерге сәйкес құрамалар алынады(асты сызылады).

2. Осы құрамаларға сәйкес дизъюнкция жазамыз. Егер х_і аргументінің құрамадағы мәні 0-ге тең болса ол конъюнкцияға өзгеріссіз енеді, ал х_і=1, болса конъюнкцияға оның терістеуі алынады.

3. Алынған барлық дизъюнкциялар конъюнкциямен жалғастырылады.

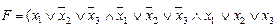
Анықтама. Егер f^*(x₁,x₂,…,x_n)= 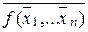онда f*(x₁,x₂,…,x_n) функциясы f(x₁,x₂,…,x_n) функциясына түйіндес функция деп аталады. f(x₁,x₂,…,x_n) функциясына түйіндес функцияны анықтау үшін, барлық айнымалылар және функцияның өзін оның қарама-қарсы мәндеріне ауыстыру керек.

Мысал. Үш айнымалыдан тәуелді 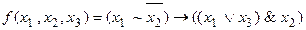функциясын буль формуласы яғни МДҚФ-түрінде өрнектеу керек.

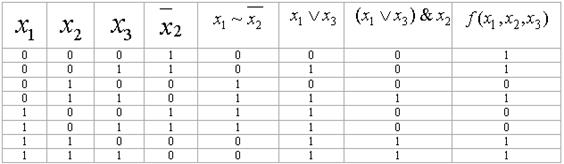
Іздеп отырған МДҚФ

=

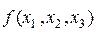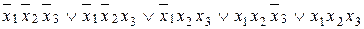
Түйіндестік принципі: Егер f функциясын өрнектейтін F формуласындағы барлық операция белгілерін түйіндес функцияның операция белгілеріне алмастырғаннан алынған F* формуласы берілген f функциясының түйіндес функциясын өрнектейтін болады.

Тек &, Ú, а, ж символдарымен ғана байланысқан формулаларды қарастырамыз. &, Ú, а, ж символдары бір біріне түйіндес деп аталады.

Мысалдар: ақиқат–формуласының түйіндесі - жалған;

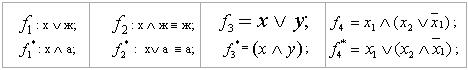
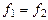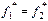Егер f₁, f₂ функциялары тең болса, онда оларға сәйкес түйіндес формулалар да тең болады. онда . Түйіндестік принцип дизъюнкция, конъюнкция, терістеу арқылы байланысқан формулалармен берілген функциялардың түйіндестерін табу үшін ыңғайлы. Бұл жағдайда берілген формулада конъюнкция дизъюнкцияға, дизюнкция конъюнкцияға ауысады. Сөйтіп ДҚФ–КҚФ, КҚФ-ДҚФ, МДҚФ–МКҚФ немесе керісінше.

Мысалы: (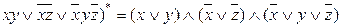

Егер j формуласы m-ге эквивалент болса:j~m онда оларға сәйкес түйіндес формулалар да эквивалентті болады ,яғни j* ~m* болады.

Егер f* (x₁,x₂,…,x_n)=f(x₁,x₂,…,x_n) онда f(x₁,x₂,…,x_n) функциясы өзіне-өзі түйіндес функция деп аталады. Мысалы, j =xyÚxzÚyz функциясы өзіне өзі түйіндес функцияны кескіндейді. Оған (б₁,б₂,б₃) және (1-б₁, 1-б₂ , 1-б₃) жиынтықтарының қарама-қарсы мәндерінде функция да қарама-қарсы мән қабылдайтындығына көз жеткізуге болады. Ол үшін ақиқаттық кесте құрып:

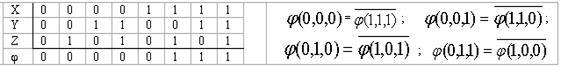
екендігін көреміз.

Мысал: Түйідестік принципіне сүйене отыра, буль алгебрасындағы түйідестік принципінің дұрыстығын дәлелдеу керек. Буль алгебрасында 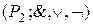үш амал бар: ;

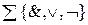Буль алгебрасының әр бір амалына түйіндес амалдарды анықтайық.

а) Айталық, 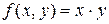болсын.

Олай болса ;

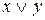б) Айталық, 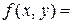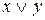;Олай болса ;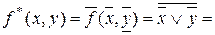

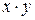в) Айталық, 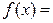; Олай болса ;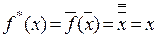

Сонымен конъюнкция дизъюнкцияға, дизъюнкция конъюнкцияға түйіндес, ал терістеу өзіне өзі түйіндес.

Негізгі әдебиет: 1[49-54]; 2[192-197].

Қосымша әдебиет: 7[50-80] .

Бақылау сұрақтары:

1. Қандай функциялар бір-біріне түйіндес деп аталады? Мысал келтіріңіз.

2. Ақикаттық кесте бойынша формула құру ережелері

8-дәріс тақырыбы: Буль функцияларының толық жүйелері. Пост теоремасы (2-сағ)

Дәріс конспекті:

Буль функцияларының толық жүйелері.Кез келген логикалық функция өрнектелетін логикалық операциялардың жиынтықтары болады. Мұндай операциялар жиыны функционалды толық жүйелер немесе базис деп аталады. Функционапды толық жүйелерге немесе базистерге мысалдар.

{&, Ú, ù}; {&, ù}; {Ú,ù}; {|}; {¯}; {&,Å,1}; {®,ù}; {Ú,~,Å}; {&, ~, Å}; т.б

Бұлардың ішінде көбірек зерттелгені {&, Ù, ù}-базис; Бұлар буль формулалары деп аталады.

Анықтама. Логикалық функциялар жиыны Р₂-негізгі жиыны, ал операциялары-дизъюнкция, конъюнкция, терістеу болатын {Р₂; &, Ú, ù} алгебрасы логикалық функциялардың бульдік алгебрасы деп аталады.

1-Теорема. Кез келген логикалық функция буль формуласы түрінде кескінделеді яғни дизъюнкция, конъюнкция, терістеудің суперпозициясы. Бұдан буль формулаларының жүйесі S={&, Ú, ù}; функциональды толық жүйе. Бұл кесте түрінде берілген кез келген функцияны буль алгебрасының формуласы түрінде кескіндеуге болатындығын көрсетеді.

2-Теорема. Егер функционалды толық S* жүйенің барлық функциялары S-жүйенің формулалары арқылы өрнектелетін болса,онда S-жүйе де функционалды толық жүйе болады.

Кез келген жүйенің толықтығы туралы сұраққа Пост теоремасы жауап береді:

Пост кластарының анықтамасы.

Р₀–класы. Бұл 0-ді сақтайтын буль функциялары класы, яғни f(0,0,…,0)=0 болатын функциялар. Р₀= {f | f (0,0,…,0) = 0}.

Р₁–класы. 1-ді сақтайтын функциялар класы, яғни f (1,1,…,1) =1 болатын функциялар. Р₁= {f | f (1,1,…,1) = 1}

S-өзіне-өзі түйіндес функциялар класы. S={f | f-өзіне-өзі түйіндес функция}

М–монотонды функциялар класы. Кез-келген (a₁, ...,a_n) және (b₁, b₂,...,b_n) нөлдер мен бірлер жиынтығында a₁ 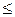b₁,...,a_n 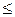b_n шарттың орындалуынан

f(a₁,…,a_n) 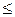f(b₁,…,b_n) орындалса f(х₁,х₂,…,х_п) функциясы монотонды деп аталады. М={f | f–монотонды функциялар}.

5. L-сызықты функциялар класы.

Егер буль сақинасында <{0,1}, Å, ã> f-функциясы f(х₁,х₂,…,х_п)=c₀Åc₁x₁Åc₂x₂Å…Åc_nx_n түрінде өрнектелетін болса, мұндағы с₁,с₂,...,с_n 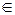{0,1} онда Буль функция сызықты деп аталады. c₀с₁с₂,...,с_n коэфициенттері төмендегідей анықталады.

с₀=f(0,0,…,0), c₀Åc₁=f(1,0,…,0), c₀Åc₂=f(0,1,…,0),...,c₀Åc_n=f(0,0,…,1) яғни с₀ =f(0,0,…,0), c₁=c₀Åf(1,…,0),…,с_n=c₀Åf(0,0,…,1)

Сонымен f–функциясының сызықтығын тексеру деген с_i коэфициенттерінің тауып, берілген формуланың ақиқаттық кестесімен табылған c₀Åс₁х₁Å...Åc_пх_п формуланың ақиқат кестесін салыстыру болып табылады. Мысалы. xÚy функциясы сызықты ма ?

Тексеру: c₀=oÚo=o; c₁=c₀Åf(1,0)=0Å(1Ú0)=1; c₂=0(f(0,1))=0Å(0Ú1)=1;

Сонымен c₀Åc₁хÅc₂y=xÅy; x v y пен xÅy ақиқат кестесі бірдей емес. Ендеше x v y–cызықты емес. Егер функцияның МДҚФ тұріндегі V–операциясының орнына Å қойылса онда сызықты функцияның мүлтіксіз полиномды қалыпты түрін аламыз. (МПҚФ) (дизъюнкция белгісінің орнына Å). Бұл Жегалкин полиномы деп аталады.

Мысалы. F(x₁,x₂,x₃)=(x₂~x₃)Ú(x₁¯x₂) функциясын 2 модулі бойынша қосу полиномы түрінде жазу керек.

f(x₁, x₂, x₃)=( 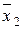Úx₃)Ú(x₁Úx₂)º(x₂, Åx₃, Å1)Ú(x₁Åx₂, Åx₁x₂)º(x₂, Åx₃, Å1)Ú (x₁Åx₂Åx₁x₂Å1)º(x₂, Åx₃,Å1)ºÅx₁Åx₂Åx₁x₂Å1Å(x₂, Åx₃,Å1)&(x₁Åx₂Åx₁x₂Å1)= x₁Åx₃Åx₁x₂Åx₁x₂Åx₂Åx₁x₂Åx₂Åx₁x₃Åx₂x₃Åx₁x₂x₃Åx₃Åx₁Åx₂Åx₁x₂Å1=Åx₂Åx₁x₃Åx₂x₃Åx₁x₂x₃Å1

(P₂, &, Å, 1)–Жегалкин алгебрасы деп аталады. å={& ,Å,1} болып белгіленеді:

сигнатура деп аталады.

Анықтама. Егер Жегалкин көпмүшелігінің құрамында айнымалылардың көбейтіндісі бар болса, онда көпмүшелік сызықты емес деп аталады, жоқ болса сызықты деп аталады.

Буль функциясының сызықтылығы Жегалкин көп мүшелігінің сызықтылығымен эквивалентті яғни Жегалкин көпмүшелігі сызықты болса оған сәйкес буль функкциясы да сызықты болады.

Мысал. f(x₁y)=x|y функциясы Пост класстарының қайсысына жататынын анықтау керек.

f(0,0)=1; f(1,1)=0, f(x₁y)ÏP_o және f(x₁y)ÏP₁

f(1,0)¹f(0,1) болғандықтан f(x, y)ÏS;

f(0,0)>f(1,1) болғандықтан f(x, y)ÏM;

f(x, y) функциясы үшін Жегалкин көпмүшелігі f(x, y)=x| y=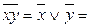

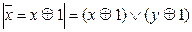=(xÅ1)Ú(yÅ1)сызықты емес. Мынадай кесте құруға болады:Пост теоремасы Буль функциялар жүйесі Ғ толық жүйе болады тек сонда ғана, егер әрбір P0, P,S,M,L кластары үшін Ғ жүйесінен осы класқа жатпайтын функция табылса.

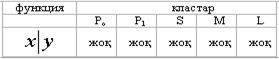
Бұл теоремадан жоғарыдағы 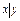функция толық жүйе құрады, яғни Шеффер функциясы арқылы кез келген буль функциясын алуға болады:

х~x|x, xÙy~ 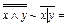~(x|y)(x|y)

Буль функциялар жүйесі толық болса базис деп аталады, ал жүйеден кез келген функция алынып тасталса жүйе толық емес болады.

Теорема. Әрбір базис 4-тен артық емес буль функциясынан тұрады.

Мысалы.

{Ù,ù }, {Ú,ù }, {®,ù }, {¯ }, {| }, { «, v, 0 },{ Å, Ù, «} базистер.

1-мысал. (P₂, &, Å, 1)–Жегалкин алгебрасындағы å={&, Å, 1} сигнатурасы функционалды толық жүйе. Бұл кез келген логикалық функция å сигнатурамен кескінделетіндігін,яғни кез келген логикалық функция айнымалылар мен {&,Å,1} операция символдары арқылы өрнектелетіндігін көрсетеді. {&, Å,1} –функцияналдың толықтығын дәлелдеу үшін.

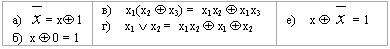
қатынастары қолданылады. Формулалардың эквиваленттігін дәлелдеудің стандартты әдісін қолданып,бұл қатынастардың дұрыстығына көз жеткізуге болады.

Бірінші теоремадан Буль функцияларының жиыны S*={&, Ú, ù}-функционалды толық. 2-теорема бойынша å={&,Å,1} жүйесінің толықтығын дәлелдеу үшін S*={&, Ú, ù}-базистің операцияларын å={&, Å,1}-базистің операциялары арқылы өрнектеуге болатындығын көрсету жеткілікті. Конъюнкция (&) операциясы екі жүйеге де ортақ. Енді қалған операциялардың (дизъюнкция (Ú), терістеу(ù )) {& ,Å,1}-символдары арқылы өрнектелетіндігін көрсетсек жеткілікті. Бұл жоғарыдағы а),г) қатынастарынан көрініп тұр.

Негізгі әдебиет: 1[49-54]; 2[192-197].

Қосымша әдебиет: 7[50-80] .

Бақылау сұрақтары:

2. Пост кластарының әрқайсысына анықтама беріңіз.

3. Логикалық функциялардың қандай жүйелері толық деп аталады?

4. Функционалдық толықтығы туралы Пост теоремасы қандай?

5. Қандай логикалық функциялар сызықты деп аталады ?

6. Жегалкин алгебрасына қандай логикалық функциялар кіреді?