Шеннон жіктелулері.

Кез келген Буль функциясы Шеннон жіктелуі түрінде өрнектеледі.

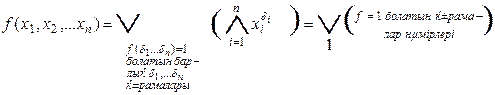Мысалы, 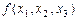000, 010, 011 құрамаларында 1-ге тең болсын. Олай болса, 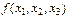жіктелуі: 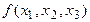= 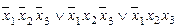; Осыған ұқсас 0-ге тең емес 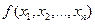функциялары төмендегідей болып жіктеледі:

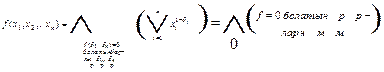
Бұл формулалардан төмендегі теореманы келтіруге болады.

Теорема.Кез келген Буль функциясын өрнектейтін формула табылады Егер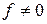

болса оны МДҚФ түрінде өрнектейтін жалғыз ғана формула бар.

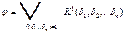
Егер 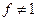болса оны МКҚФ түрінде өрнектейтін жалғыз ғана формула бар.

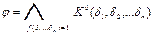
Мысалы, ақиқаттық кестемен берілген 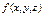функциясының МДҚФ, МКҚФ табу керек. Функцияның толықтығы туралы теорема бойынша

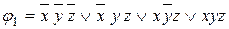-МДҚФ;

-МКҚФ

Сонымен МДҚФ, МКҚФ - белгілері.

Дизъюнкцияның (конъюнкцияның ) мүшелері әр түрлі конъюнктердің (дизъюнктердің) мүшелері әр түрлі бір де бірі конъюнкте (дизъюнкте)айнымалының әрі өзі ,әрі оның терістеуі бірге болмайды.

Әрбір конъюнктің (дизъюнктің ) құрамында формулаға енетін барлық айнымалылар болуы керек, яғни х₁^aÙх₂^aÙ...Ùх₃^a мұндағы х_і^a не 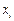өзі , не .

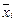Мысалы, 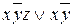-өрнегі 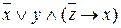формуласының – дизъюнктивті қалыпты формаларының бірі. Бұл МДҚФ-ң алдыңғы үш талабын қанағаттандырады, ал төртіншісін қанағаттандырмайды. Сондықтан оған түрлендірулер жүргіземіз ( 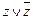көбейтміз).

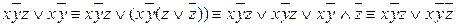
Кез келген F (х₁,х₂...х_n) формуласын МДҚФ (МКҚФ ) түріне келтіру үшін мына ережені қолдануға болады.

F (х₁,х₂...х_n ) формуласын қандайда бір дизъюнктивті (конъюнктивті) қалыпты формаға түрлендіру.

Егер конъюнктке қандай да бір айнымалы өзінің терістеуімен бірге кірсе оны ДҚФ- тан жою керек. (х Ù 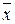= 0)

Егер конъюнктке бір литер х^a бірнеше рет кірсе, олардың біреуін ғана қалдырып калғандарын қысқарту керек. (х Ù х= х)

Егер конъюнктердің біріне ( 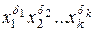) y айнымалыc кірмей тұрса, онда бүл конъюнктті оған эквивалентті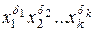 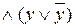формуламен алмастырамыз да, дистрибутивті заңды (xÙ (yÚz)) = xy Ú xz қолданып ДҚФ түріне келтіреміз. Егер толық емес конъюнкт бірнешеу болса олардың әрқайысысы үшін сәйкес 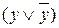формуласын қосамыз.

Алынған ДҚФ-да бірдей бірнеше конъюнктер болса олардың ( х 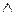х) біреуін ғана қалдырамыз. Нәтижесінде МДҚФ шығады.

Мысалы, 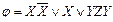ДҚФ –ны МДҚФ-қа түрлендіру керек.

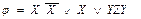
[дистрибутивтік заңымен ашамыз]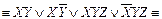

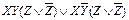
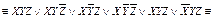
КҚФ-ны МКҚФ түрлендірудің алгоритмі де осындай. Мысал арқылы көрейік. 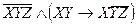формуланы МКҚФ ға келтіру керек болсын.

1.Формуланы қандайда бір конъюнктивті қалыпты формаға (КҚФ) келтіреміз.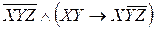

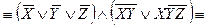
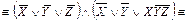
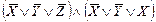
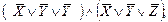
2). Бірдейлерін жоямыз. Айнымалының терістеуімен бірге қатысып тұрған конъюнкция мүшесі,3 қайталанып тұрған конъюнкция мүшесі 1 мен 4.

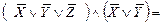ТОЛЫҚТЫРАМЫЗ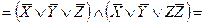

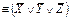
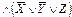
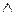
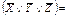
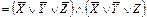-Бұл МДҚФ

Негізгі әдебиет:2[180-185]; 3[172-193].

Қосымша әдебиет::7[50-80]

Бақылау сұрақтары:

1. Буль функцияларының негізгі қасиеттерін атаңыз.

2. Логикалық функцияларды жіктеу туралы Шеннон теоремасы қандай?

3. Буль алгебрасындағы негізгі эквиваленттік түрлендірулерді атаңыз.

4. Функцияның МДҚФ,МКҚФ қалай табуға болады ?

5. Қандай логикалық функцияда МДҚФ болмайды?

7-Дәріс. Ақиқат кесте бойынша берілген. Буль функциясына формула құру әдісі. Буль функцияларының түйіндестік принципі.(2сағ).

Тұжырымдар логикасының әрбір формуласына ақиқат кесте құруға болатынын білеміз. Керісінше қалай?. Керісінше де яғни ақиқат кесте бойынша формула құруға болатынын көреміз.

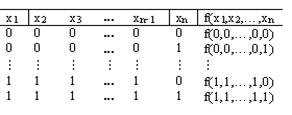
2. Осы құрамаларға сәйкес конъюнкция жазамыз. Егер х_і аргументінің құрамадағы мәні 1-ге тең болса ол конъюнкцияға өзгеріссіз енеді, ал х_і=0, болса конъюнкцияға оның терістеуі алынады.

3. Алынған барлық конъюнкциялардың дизъюнкциясы іздеген формула болады және ол құрылған функцияның МДҚФ-ы болады.

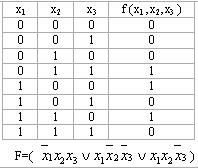
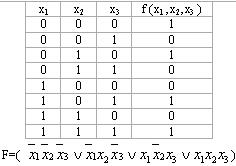
Мысалы, f (x1 ,x2,x3 )= 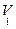(3,4,6), f (x1 ,x2,x3 )= 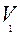(0,2,5,7)

3,4,6-құрамалардың нөмірлері 0,2,5,7- құрамалардың нөмірлері