Орналастыру және функционал бейнелеу.

Комбинаторикалық классикалық есептерінің бірі, қандай да бір объектілердің «жәшіктерде» белгілі бір шектеулер орындалатындай орналастыру санын анықтау болып табылады. Бұл есепті төмендегідей тұжырымдауға болады:

Айталық |Х| = r, |Y| = n. Барлық бейнелеулер f : X ® Y санын Y^Х белгілейік. Берілген шектеулерді қанағаттандыратын қанша f : X ® Y функционал бейнелеулер бар? Егер бұл бейнелеулерге шектеулер жоқ болса төмендегідей тұжырым келтіруге болады.

5-тұжырым.| YХ | = 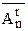= nr = |Y||X|.

Шынында, Х={x₁,…,x_r} болсын. Олай болса кез келген бейнелеуді f:Х®Y реттелген (f(x₁), f(x₂),…,f(x_r)), мұндағы f(x_i)ÎY, тізбегі түрінде кескіндеуге болады, яғни біз функционал бейнелеулер мен саны n^r-ге тең, көлемі n болатын Y жиынынан алынған қайталанба реттелген таңдамалар жиынының арасында өзара бір мәнді сәйкестік орнаттық.

(Егер Х - объектілер, Y- "жәшіктер" болса, онда f функция әрбір хÎХ объектісі үшін объект орналасқан f(x)ÎY жәшігін көрсетеді).

Бірден артық емес объект орналасқан жәшігі бар орналасудың санын табу қиын емес, ондай теру бір мәнді функцияларға сәйкес (инъективті бейнелеу).

6-тұжырым. Иньективті бейнелеулердің f:X®Y(яғни f(x₁)=f(x₂)®х₁=х₂) саны .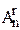

Шынында да, бұл жағдайда реттелген тізбек (f(x₁), f(x₂), …, f(x_r)) әр түрлі болуы керек, яғни бұл тізбек қайталанбайтын теру болып табылады.

Салдар. Егер Sn - өзіне өзін бейнелейтін n-элементті барлық биективті бейнелеулердің жиыны болса олардың саны |Sn|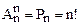

Негізгі әдебиет: 1[130-134]; 2[159-164].

Қосымша әдебиет: 7[50-80] .

Бақылау сұрақтары:

Қосу, көбейту ережелерін атаңыз.

Реттелген, реттелмеген таңдамалар қалай аталады?

Орналасу, теру сандарын қандай формулалармен есептеуге болады?

Қанша функционал бейнелеулер f : X ® Y бар?

Өзіне өзін бейнелейтін қанша биективті бейнелеу құрастыруға болады?

10-Дәріс тақырыбы: Жиындарды бөліктеу. (2 сағат)

Дәріс конспектісі:

n-элементті жиынды k ішкі жиынға бөліктеу деп , 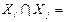Æ, i¹j Хi¹Æ, i= 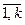орындалатын { X1, X2, …, Xk } кез келген жиындар үйірін түсінеміз. Х-ті к блокқа бөлетін бөліктеулер жиынын Пк(х) деп белгілейік. |Пк(х)|. Бұдан әрине, S(n, k)=0 үшін k>n; S(0, 0)=1 деп алынады. n-элементті жиынды К блокқа бөлетін бөліктеулер санын S(n, k) = |Пк(х)| белгілейміз.

1-тұжырым. S(n, k)= S(n-1, k-1)+k×S(n-1, k) егер 0<k<n; S(n, n)=1 егер n³0 ; S(n, 0)=0 егер n>0. S(n, k) саны II ретті Стирлинг саны деп аталады. Шынында да бірінші және үшінші формулалар түсінікті: 1 формуланы дәлелдеу үшін {1, 2, …, n} жиынын к блокқа бөлетін барлық бөліктеулердің жиынын қарастырамыз. Бұл жиын үлкен 2 класқа бөлінеді: бір элементті {n} блогы бар бөліктеулер және n-қуаты 1 деп үлкен блоктың элементі болып саналатын бөліктеулер. Бірінші класта S(n-1, k-1) блок бар, ал екіншісінде S(n-1, k). Себебі бұл кластың {1, 2,…,n-1} жиынын к блокқа бөлетін әр бөліктеуінде бұл класта әр блокқа кезекпен n элементін қосудан алынған к бөліктеуі сәйкес келеді. Мысалы, S(4, 2)=S(3, 1)+2S(3, 2)=1+2(S(2, 1)+2S(2, 2)) =1+2(1+2)=7.

Егер Х={1, 2, 3, 4} онда бұл жиынды 2 блокқа бөлетін 7 бөліктеу төменгідей:

{{1, 2, 3}, {4}}; {{2, 3, 4}, {1}}; {{1, 2, 4}, {3}};{{1, 2}, {3, 4}};

{{1, 3, 4}, {2}};{{1, 4}, {2, 3}}; {{1, 3}, {2, 4}}; II ретті Стирлинг сандарын үшбұрышты кесте түрінде орналастыруға болады:

Кестенің шеткі бірлерден басқа әр элементі есептелетін элементтен жоғарғы жолда орналасқан санды к-ға көбейтіп, оның сол жағындағы элементпен қосқаннан алынады.

Енді ақырлы Х жиынын Х₁, Х₂, …, Х_k (k³1) (мұндағы әр X_i n_i элементтен тұрады) ішкі жиындарына бөлетін бөліктеулердің санын анықтайық:

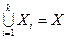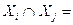, Æ , i¹j |Х_i|=n_i, 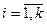; спектісі.ы. ады. екені белгілі. Кейбір i нөмірі үшін Х_i =Æ болуы мүмкін. Тұрақатн n_i үшін бөліктеулер санын 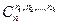деп белгілейік (Мұндағы бөліктеулердегі ішкі жиындар жиынтығы реттелген жиындар тізбегі болып табылады.

2 - тұжырым. .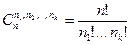

Шынында да, әрбір Х_i ішкі жиынын қайталанбайтын теру деп қарауға болады, олай болса,

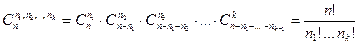
Мысал. 25 адамнан тұратын топқа староста сайланды. 12 адам келісті, 10 қарсы болды, 3-і қалыс қалды. Мұндай сайлау қанша әдіспен жүргізіледі?

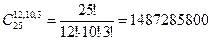
Енді i=1, 2, …, n үшін әрқайсысында i элементі бар mi ішкі жиыны бар болатын 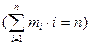|X|=n, Х жиынын қанша ішкі жиынға бөлуге болатынын есептейік: Мұнда алдыңғы жағдайға қарағанда ішкі жиындарды таңдау реттелмеген. Мысалы, Х = {1, 2, 3, 4, 5}жиыны үшін келесі үш бөліктеу бірдей.

{1, 3}, {4}, {2, 5}; {4}, {2, 5}, {1, 3}; {2, 5}, {4}, {1, 3}

Бұл бөліктеуде m₁=1, m₂=2, m₃=m₄=m₅=0.Аталған бөліктеулердің санын N(m₁, m₂, …, m_n) арқылы белгілейміз. 3 - тұжырым.

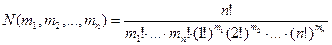
Қарастырылып отырған реттелмеген бөліктеудің әрқайсысын m₁!×m₂!×…×m_n! тәсілмен төмендегі реттелген бөліктеуге түрлендіруге болады:

мұндағы,

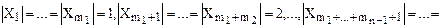
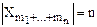. Мұндай реттелген бөліктеудің саны: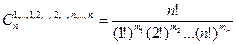

Ал реттелмеген бөліктеудің саны бұдан m₁!×…×m_n! есе аз.

Мысал. 25 адамнан тұратын топты әрқайсысы 5 адамнан 5 коалацияға қанша әдіспен топтастыруға болады? |X| = 25, m₁=…=m₄=0, m₅=5, m₆=…=m₂₅=0;

N(0, 0, 0, 0, 5, 0, …, 0) = 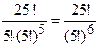=5194672859376.

Ендіру және шығару формуласы. Жиындарды бөліктеуАйталық, Х₁, Х₂– ақырлы жиындар берілсін. Егер Х₁ÇХ₂=Æ, онда | Х₁ÈХ₂| = | Х₁|+|Х₂|. Егер Х₁ÇХ₂¹Æ, онда |Х₁|+|Х2| жиынында Х₁ÇХ₂ алынған элемент 2-рет есепке алынады, демек |Х₁ÈХ₂|=|Х₁|+|Х₂|-|Х₁ÇХ₂|.

Кез келген жиын үшін ендіру және шығару формуласын қорытайық:

4-тжырым. Х_i; i=1,…,n, n³2 ақырлы жиындары берілсін. Олай болса |X₁ÈX₂È…ÈX_n|=(|X₁|+…+|X_n|)–(|X₁ÇX₂|+|X₁ÇX₃|+…+|X_n-1ÇX_n|)+(|X₁ÇX₂ÇX₃|+ …+|X_n-2ÇX_n-1ÇX_n|)-…+(-1)ⁿ⁺¹|X₁ÇX₂Ç…ÇX_n|.

Салдар. Айталық Х – ақырлы жиын болсын, Х₁, …, Х_n – Х-тің ішкі жиындары. Онда ішкі жиындардың ешбіріне тиісті емес хÎХ элементтердің саны мына

|X\(X₁ÈX₂È…ÈX_n)|=|X|-(|X₁|+…+|X_n|)+(|X₁ÇX₂|+… |X_n-1ÇX_n|)-…-

(-1)ⁿ|X₁Ç…ÇX_n| формула бойынша есептеуге болады.

Ендіру және шығару формуласын жазудың кең тараған формасы төмендегідей. Айталық, Х N элементтен тұратын ақырлы жиын, a₁,…, a_n Х-тің элементтерінде бар болуы да, болмауы да мүмкін қасиеттер. X_i арқылы a_i қасиеттері бар элементтерден құралған жиынды белгілейміз. Яғни Х_i = {xÎX | a_i(x)}, i=1…, n.

N( 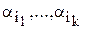) арқылы 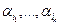қасиеттерінің бәріне ие Х элементтерінің санын белгілейік:

N( 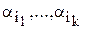)=| |. a₁,…,a_n қасиеттердің ешқайсысы жоқ элементтің санын N₀=|X\(X₁È…ÈX_n)| деп белгілейік.

Олай болса N0=N–S1+S2-…+(-1)nSn=N+ ,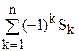

мұндағы S_k= , k=1,…,n.

Мысалы, егер n=3,онда N₀=N–N(a₁)–N(a₂)–N(a₃)+N(a₁,a₂)+N(a₁, a₃)+N(a₂,a₃)–N(a₁, a₂, a₃).

Мысал. Айталық, Х={1,2,…,10}, a₁(x):"х–жұп", a₂(х):"x>6", a₃(x): "2<x<8" болсын. Ешқандай қасиеті жоқ элементтердің саны N₀ есептейік. N₀ = 10-5-4-5+2+2+1-0=1 (шынында, Х-ң ешқандай қасиеті жоқ элементі 1 a_i, i = 1, 2, 3).

Ендіру және шығару формуласын шығарып пайдаланатын тағы бір есепті қарастырайық.

Тәртіпсіздік туралы есеп. Әр түрлі а₁, а₂, …, a_n n зат және әр түрлі

b₁, b₂,…, b_n жәшіктер бар. a_i заттарының ешқайсысы b_i жәшігіне түспейтіндей етіп, a_i бұйымдары қанша әдәспен жәшіктерге салуға болады? Басқаша айтсақ, кез келген i=1, 2, …, n үшін a_i¹i болатындай

1, 2, …, n сандарының қанша алмастырулары a₁, a₂, …, a_n бар? Яғни кез келген элементтің образы өзінің образына тең болмайтындай қанша алмастыру бар?

Берілген Х жиыны ретінде бұйымдардың жәшіктерге барлық мүмкін орналасуларының жиынтығын аламыз.Олай болса N=| X |=n! ai қасиеттерін енгізейік: "ai bi жәшігінде бар", i=1,…,n. 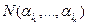) саны aij бұйымы b_ij j=1,…,k жәшігінде бар болатын орналасулар (n-k)!-ға тең.

Бірақ онда k бұйымның өздерінің S_k жәшіктеріне түсетін орналасулар саны:

S_k =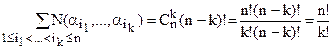

Енді ендіру және шығару формуласын пайдаланып, ешқандай қасиет орындалмайтын (яғни ешқандай ai бұйымы bi жәшігіне түспейді) орналасу саны:

N₀=N+ .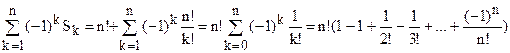

Жақшадағы өрнек - е-1 шексіз қатар жіктеуінің 1-ші мүшелері, ендеше

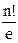-n символдан тұратын тәртіпсіздіктер санына жақсы жуықтайды.

Егер бізді тәртіпсіздіктің саны ғана емес, а_i=i дәл k орында болатын,

1, 2, …, n құралған а₁,…,a_n алмастырулардың санын да анықтау керек болса, онда «кездесу» деп аталатын басқа есеп туады. Оның шешімі: n-нен k санды 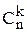тәсілмен таңдауға болады, таңдағаннан кейін оны қалған n-k символдағы тәртіпсіздіктердің санына көбейту керек. Сонда

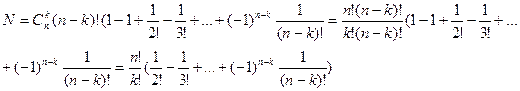
Негізгі әдебиет: 1[136-143]; 2[164-166].

Қосымша әдебиет: 7[50-80] .

Бақылау сұрақтары:

1.Сізге жиындарды бөліктеудің қандай типтері белгілі?

2. Стирлинг саны қалай есептеледі?

3. 4 жиын үшін ендіру және шығару формуласын құрыңыз.

4. Тәртіпсіздік туралы есепті сипаттаңыз.

5. Кездесу есебін келтіріңіз.

11-Дәріс тақырыбы: Графтар. Қасиеттері. Операциялар. (2 сағат)

Дәріс конспектісі: