Салмақтанған графтар.

Көп есептерде графтардың төбесі мен доғалары туралы қосымша ақпарат қажет болады, мысалы, егер граф қалааралық жолдарды бейнелесе салмақтанған графтар қолданылады.

Айталық S_M, S_R - таңбалар жиыны болсын. f: M→S_M (төбелерді таңбалау), g: R→S_R (доғаларды таңбалау) функциялары G=<M,R> графын таңбалау бөлінуі деп аталады. G=<M,R,f,g> таңбаланған немесе салмақтанған граф деп аталады.

f(a)-a төбесінің салмағы деп, ал g(e) e доғасының салмағы деп аталады. Доға мен төбенің біреуінің ғана таңбалануы жиі кездеседі.

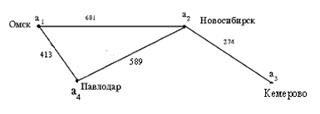
Мысалы: Айталық M={a₁, a₂, a₃, a_n}, R={[a₁a₂], [a₂ a₃], [a₁ a₄], [a₂ a₄]};

f:M→C мұндағы, С- қалалар жиыны, g:R→W.

f(a₁)=Омск, f(a₂)=Новосибирск, f (a₃)=Кемерово, f (a₄)=Павлодар

g([a₁ a₂])=681; g([a₂ a₃])=274, g([a₁ a₄])=413; g([a₂ a₄])=589. Таңбалаған <M,R,f,g> графты–белгілі бір қалалар арасындағы ұзындығы көрсетілген автомобиль жолдарының схемасы. Салмақталған графтардағы доғалардың салмағы туралы ақпаратты салмақ матрицасы арқылы кескіндеуге болады. W=( 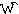_ij) – мұндағы 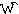_ij – (a_i,a_j) доғасының салмағы жоқ доғалар әдетте ноль немесе 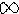белгісімен белгіленеді. Қарастырылған мысал үшін салмақтылық матрицасының түрі