Графтарға қолданылатын амалдар. Графқа төбе қосу.

G=<M,R> графына а төбесін қосқаннан <М 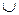{a}, R> графы құралады.

Графқа доға қосу операциясының нәтижесінде <М 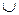{(a,b)}, R 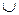{(a,b)}> графы құрылады.

Графтан доға алу–R доғалар жиынынан (a,b) жұбы алынады. <M,R\{(a,b)} >

Графтан төбе алуоперациясының нәтижесінде. G графынан а төбесі оған инцидентті доғалармен бірге алынады деп айтады. <M\{a}, R\{(b,с)│ b =a немесе c = a}>

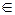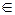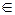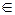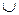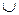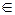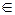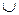Графтың a,b төбелерін теңестіру деп графтан a,b төбелерін алып тастап мына тәртіппен төбе мен қабырға қосу: жаңа а¹ төбесі мен (а¹, с), егер (а, с) R немесе (b, с) R және (с, а¹) доғасын егер (с, а) R немесе (с, b) R болса:<(M\{a,b}) {a¹}, (R\{(с, d)│c=a немесе d=a, немесе c=b, немесе d=b}) {(a¹,c)│(a, c) R, немесе (b, c) R} {(c, a¹)│(c, a)R, немесе (c, b) 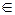R}).

Алынған граф G графынан a,b төбелерін теңестіргеннен алынды делінеді.

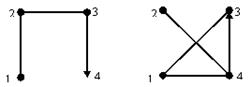
a,b төбелері доғамен қосылса, төбелерді теңестіру a,b доғасын созғаннан алынады дейді. Мысалдар: Берілген=<{1,2,3,4},{[1,2],[2,3],,(3,4)}> графынан суреттегі G₁-G₆ графтары қандай операциялармен алынды?

G графына 5 төбені қосқаннан G₁ графы алынды.

G графына (3,1)–доғасын қосқаннан G₂ графы алынды.

G графына (3,2) доғасы алынады G₃ графы алынды.

G графына 2 – төбені алғаннан G₄ графы алынды.

G графының (1,4) төбелерін теңестіргеннен G₅ графы алынды.

G графының (2,3) доғасын қысқаннан G₆ графы алынды.

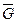=<M, М²\R 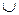Id_М> графы ілгексіз G=<M,R> графының толықтырушы графы деп аталады.

Мысал: Айталық, G₁=<M₁,R₁>, G₂=<M₂,R₂> графтары берілсін.

G= <M,R>; 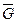=<M, М² \R 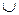Id_М>

Анықтама: G₁, G₂ графтарының бірігуі деп G₁UG₂=<M₁UM₂,R₁UR₂> графын айтады.

Анықтама:ЕгерМ₂∩М₂= 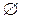онда G₁,G₂ графының қиылысуы деп, G₁∩G₂=<M₁∩M₂,R₁∩R₂> графын айтады.

Анықтама: G₁, G₂ графтарының сақиналы қосындысы деп G₁ 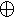G₂=<M₁UM₂,R₁ 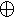R₂>, мұндағы R₁ 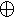R₂=( R₁\R₂)U(R₂ \R₁).

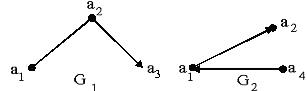
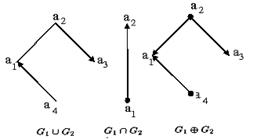
Мысалы G₁ және G₂ графтары берілсін.

G₁= < {a₁, a₂, a₃}, {[a₁, a₂], (a₂, a₃)} >;

G₂= < {a₁, a₂, a₄}, {(a₁, a₂, ), (a₄, a₁)}>;

Табу керек: G₁U G₂, G₁∩G₂, G₁ 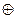G₂?

Шешуі: Анықтама бойынша:

G₁UG₂=<{a₁, a₂, a₃, a₄},{[a₁, a₂], (a₂, a₃), (a₄, a₁)}>;

G₁∩G₂ = < {a₁, a₂}, {(a₁, a₂)} >.

G₁ G₂=<{ a₁, a₂, a₃, a₄}, {( a₂, a₁), (a₂, a₃), (a₄, a₁)} >;

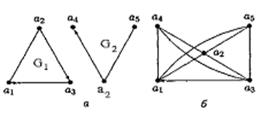
G₁, G₂ графтарының қосылуы деп

G₁+ G₂ =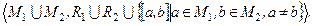

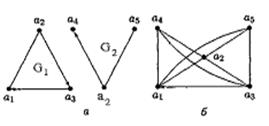
Мына суреттің а пунктіндегі G₁, G₂ графтарының қосындысы б пунктте көрсетілген.

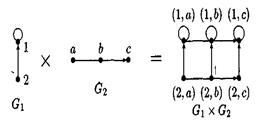
G₁, G₂ графтарының көбейтіндісі деп G₁xG₂=<M₁xM₂, R>, мұндағы ((a₁,b₁), (a₂, b₂)) 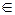R тек сонда ғана, егер a₁=a₂ және (b₁,b₂) 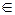R₂ немесе b₁=b₂ және (a₁,a₂) 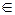R₁.