Кез келген ҚҚФ ДҚФ-қа түрлендірудің алгоритмі.

Егер формуланың ҚҚФ белгілі болса ,оны төмендегі ережемен ДҚФ түрлендіруге болады.

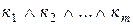
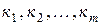Айталық, ДҚФ F= түрінде болсын. Мұндағы -элементар дизъюнкциялар.

F-ке қос терістеу F= 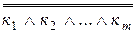заңын қолданып, 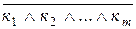-ді КҚФ –ке 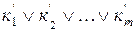түрлендіру керек. Мұндағы 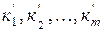- элементар дизъюнкциялар.Сонда,

F= = =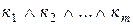

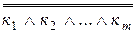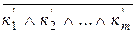
Морган заңымен екінші терістеуден құтылып элементар дизъюнкциялардың терістеулерін элементар конъюнкцияларға 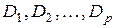түрлендіру керек.

Сонда, F= = =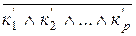

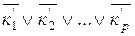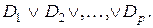
Буль функцияларының шексіз көп ҚҚФ, ДҚФ болуы мұмкін. Олардың ішінен МДҚФ,МКҚФ- ерекше ролі бар.

Мүлтіксіз дизюнктивті,конъюнктивтіқалыпты форма (МДҚФ, МКҚФ).

Анықтама. Кез келген формуланы оған эквиваленттіДҚФ-ті ҚҚФ-ке түрлендірудің алгоритмі.

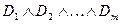
формулаға түрлендіруге болады, мұндағы 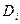-не айнымалы, не оның терістеуі немесе айнымалы мен оның терістеуінің дизъюнкциясы (конъюнкциясы). Осындай формула берілген формуланың дизъюнктивті ( конъюнктивті). қалыпты түрі деп аталады.

Мүлтіксіз дизюнктивті қалыпты форма (МДҚФ)

Анықтама. Айталық, А формуласы < 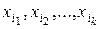> айнымалыларынан тәуелді болсын. Егер төмендегі шарттар орындалса А формуласы берілген айнымалылар тізімінде мүлтіксіз дизъюнктивті қалыпты формада делінеді.

А- дизъюнктивті қалыпты формада (элементар конъюнктер дизъюнкциясы)

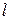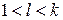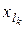А- ның әрбір дизъюнктивті мүшесі к-мүшелі конъюнкция және бұл конъюнкцияның әрбір - орында ( ) не айнымалысы не оның терістеуі орналасады. А- ның барлық дизъюнктивті мушелері өзара әртүрлі.

Мысалы, 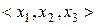-айнымалылар тізімінде ( 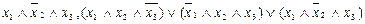-дизъюнктивті қалыпты формалар.