Суперпозициялар

Анықтама.Функция аргументтерінің орнына элементар немесе басқа да функцияларды (f₁,f₂,…,f_k) қою арқылы алынған жаңа функция (F) функциясы f₁,f₂,…f_k функцияларының суперпозициясы деп аталады.Мысалы, терістеу, коньюнкция, дизьюнкция, импликация, эквиваленция функциялары арқылы олардың суперпозициясы болып табылатын логикалық алгебраның жаңа функцияларын жазуға болады:

х₂ ® x₁ ; x₁ Ú 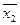; (x₁ Ú x₂) ® ( 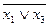); ((x ~x₃)Úх₁)®(x₂® 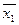) т.б

Егер формулада операция таңбасы аргументтердің арасында тұрса,ондай жазуды инфиксті жазу деп атайды. f₁=x₃Úx₁; f₂=x₁Åx₂;f₃=x₁Ù(f₂); f₄=(x₃Úx₁)Å(x₁&(x₁Åx₂));

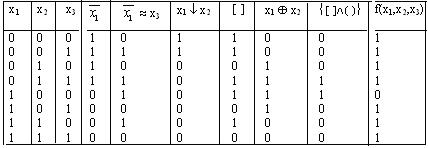
Элементар функциялардың ақиқаттық кестесі арқылы олардың суперпозициясы болып табылатын кез келген функцияның ақиқат кестесін анықтауға болады.

f(x₁,x₂,x₃) = {[( 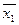~ x₃) Ú ( x₁ ¯ x₂)] ­ ( x₁ Å x₂)}® x₃ функциясын ақиқаттық кесте арқылы өрнектеу керек болсын;

Жақшаларды қою ретіне логика алгебрасында арнаулы келісімдер қабыл данған: Сыртқы жақшалар жазылмайды. Мысалы, ( (xÚу z)) өрнегінің орнына xÚу z жазуға болады. Операциялардың орындалу приоритеттері:

( ù , Ù, Ú , ® ,«, ê, ¯ , Å , );

Мысалдар:

1. xÙyÙz өрнегі ((xÙy)Ùz ) болып жазылады.

2. xÚy«z®u өрнегі ( (x Ú y ) « ( z®u ) болып жазылады.

3. xÅy« ®uÚvÙw¯xêy өрнегі ((xÅy)«( 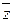®(uÚ(((vÙw)¯x)êy) болып жазылады

4. x®( 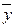®z) өрнегінде жақшаны қалдыруға болмайды. Жақшасыз жазылса (x® 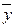)®z болып кетеді.

Логикалық алгебра функциясын бульдік функция, екілік функция (двоичная) немесе ауыстырып қосқыш (переключательная) функция деп атайды.Буль функциялары арқылы қандай да бір құрылғыға берілген сигналдардың қортынды сигналға түрленуін белгілеуге болады. Мысалы, суретте көрсетілгендей қүрылғының n нүктеден тоқ қабылдау мүмкіндігі бар. Құрылғыларға берілген токқа байланысты xi=1 айнымалының мәні тоқтың i- ші нүктеге берілуін көрсетеді, xi=0 тоқ жоқты көрсетеді. f(б1б2,...,бт) = 1 тоқтың шығу нүктесін берілуін, f = 0 болуы тоқтың берілмеуін көрсетеді.

1-мысал. коньюнкция X 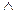Y – екі тоқ беру нүктесі, бір шығу нүктесі бар құрылғыны көрсетеді. Шығу нүктесіне тоқ беріледі, егер x,y- ке тоқ берілсе.

2-мысал. Үш адамнан тұратын комиссяның дауыс беруін белгілеп отыратын құрылғыны қарастырайық. Комиссия мүшелері резолюцияға (ұсынылған шешім) өз кнопкасын батырады.Егер комиссия мүшелерінің көпшілігі резолюцияны мақұлдаса, онда резолюция (шешім) қабылданады Бұл регистрация жасайтын құрылғымен белгіленіп отырылады

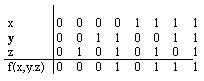
Құрылғының жұмысының ақиқаттық кестесі суретте көрсетілгендей функциямен сипатталады; алынған функцияны f(0,0,0) = f(001) = f(010) = f(100) = 0 теңдіктер жүйесімен де беруге болады.

( 0 0 0 1 0 1 1 1 )–жиынтығы f функциясының мәндер векторы деп аталады.

Қосымша әдебиет: 7[50-80] .

Негізгі әдебиет:1[46-49]; 9[194-200]

Қосымша әдебиет: 7[9-34]

Бақылау сұрақтары:

1. Қандай функциялар логикалық деп аталады?

2. Бір айнымалыдан тәуелді барлық функцияларды атаңыз.

3. n айнымалыдан тәуелді неше логикалық айнымалылар бар ?

4. Қандай айнымалылар негізгі деп аталады,қандайлары –жалған?

5. Логка алгебрасының қандай формулалары эквивалентті деп аталады?

6-Дәріс тақырыбы. Логикалық алгебра функцияларын аналитикалық түрде жазу. ДҚФ, КҚФ, МДҚФ, МКҚФ. (2сағ)

Дәріс конспектісі:

Анықтама. Егер x логикалық айнымалы, 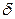Î {0,1} болса, онда 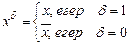өрнегі литер деп аталады. 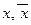литерлері контрарлы литерлер деп аталады.

Анықтама. Егер формула айнымалылар немесе олардың терістеулерінің дизъюнкциясы болса (бір мұшелі болуы да мүмкін) оны элементар дизъюнкция (дизъюнктер) деп атайды.

Мысалдар. x₂,x₃; x₁Úx₂Úx₃, x₁Úx₂Úx₃; xÚyÚz; xÚyÚx–дизъюнктер.

Анықтама. Егер формула айнымалылар немесе олардың терістеулерінің конъюнкциясы болса (бір мұшелі болуы да мүмкін)оны элементар конъюнкция (конъюнктер) деп атайды.

х₁, x₂, x₁Ùx₂ , 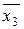, , 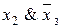, 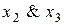x₁Ùx₂Ùx₃;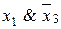

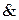
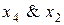
х- бір уақытта дизъюнкт те, конъюнкт те бола алады.

Анықтама. Конъюнктердің дизъюнкциясы дизъюнктивті қалыпты форма (ДҚФ Элементар конъюнкциялардың дизъюнкциясы) деп, ал дизъюнктердің конъюнкциясы конъюнктивті қалыпты форма деп аталады (КҚФ-Элементар дизъюнкциялардың конъюнкциясы).

Мысалы. ДҚФ: 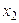, , 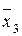, , 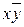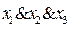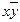Úyz,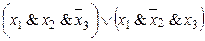

КҚФ: (xÚyÚ 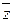)Ù(xÚz)y; – ДҚФ; 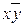- КҚФ-те ДҚФ-те бола алады.

1-Теорема. Кез-келген А формуласы үшін оған эквивалентті қалыпты дизъюнктивті формадағы В формуласын (А 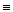В) табуға болады. В А-ның қалыпты дизъюнктивті формуласы деп аталады.Дәлелдеусіз (кез келген формула өзінің ДҚФ,КҚФ эквивалентті ).