Формуланы дизюнктивті қалыпты формаға келтірудің алгоритмі

1. Формула құрамындағы барлық логикалық операцияларды

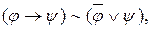
эквиваленттіліктер және ¯,Å операцияларының анықтамаларын пайдаланып дизъюнкция, конъюнкция, терістеу арқылы өрнектейміз. (Дизъюнктивті қалыпты формаға түрлендіру )

2. Морган заңын пайдаланып, барлық терістеулерді айнымалыларға көшіріп, қос терістеулерді 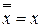формуласы бойынша қысқартамыз.

Дистрибутивті 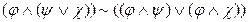заңды пайдаланып, форму-ланы барлық конъюнкциялар дизъюнкциялардан бұрын орындалатындай түр-лендіреміз. 1-3 пункттерді орындаудың нәтижесінде формула дизъюнктивті қалыпты формаға түрлендіріледі.

Мысалы, j=((x®y)¯(x®z)) формуласын дизъюнктивті қалыпты формаға түрлендіру керек болсын. ®, ¯ операцияларын Ù,Ú, - арқылы өрнектейміз.

¯

;

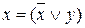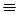
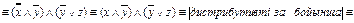
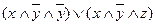Сонымен, j = (( x®y) ¯ ( x®z)) ;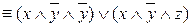

2-Теорема. Кез келген А формуласы үшін оған эквивалентті және ҚҚФ болатын В формуласын табуға болады АºВ (дәлелдейміз) В А- ның ҚҚФ. Кез келген формула өзінің ҚҚФ эквивалентті.

Конюнктивті қалыпты формаға келтірудің алгаритмі алдыңғыға ұқсас, тек 3 пунктың орнына қолданылады.

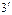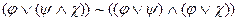. дистрибутивті заңды пайдаланып, фор-муланы барлық дизъюнкциялар, конъюнкцияларға қарағанда бұрын орын-далатындай түрлендіреміз.

Мысалы. 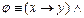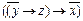формулада 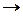болмайтындай түрлендір-еміз:

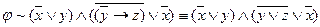
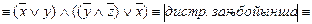
-бұл формуланы одан әрі тағы түрлендіруге болады:

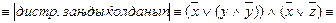
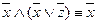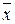; -ті ҚҚФ деуге де, ДҚФ деуге де болады. Бұлардан басқа егер формуланың ДҚФ белгілі болса ҚҚФ-ке , ҚҚФ белгілі болса ДҚФ көшудің алгоритмдері бар. Олар төмендегідей: