Модулі бойынша қосу, импликация, Шеффер және Веб операцияларының қасиеттері.
Импликация мен 2 модулі бойынша қосу функцияларының қасиеттері дискретті құрылғыларды анализдеу, синтездеу кезінде пайдалы.
2-нің модулі бойынша қосу операциясы үшін ассоциативті, коммута тивті заңдар және коньюнкцияға қатысты дистрибутивті (распределит) заңы бар.
1. x 1 Å х2 = х2 Å x1 коммутативтілік
2. x 1 Å ( х2 Å x3 ) = ( x 1 Å х2 ) Å х3 ассоциативтілік
3. x 1 & ( х2 Å x3 ) = ( x 1 & х2 ) Å ( x 1 & х2 )
бұларға қоса
1. x Å х = 0; 2. х Å 0 =х; 3. x Å 1 =  ; 4. х Å
; 4. х Å  =1;
=1;
және x 1 Ú х2 = х1 Å x2 Å x 1 & х2
x 1 Å х2 = 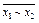 =
= 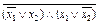
формулалары бар.
Импликация үшін коммутативті, ассоциативті заңдар жоқ.
x ® х = 1; 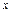 ®
® 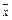 =
= 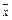 ; x ® 1 = 1;
; x ® 1 = 1;
x ® 0 = х; 0® х =1; 1 ® х = х;
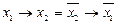 ; x 1 ® х 2 ® х1 = х1
; x 1 ® х 2 ® х1 = х1
Шеффер және Веб функциялары үшін коммутативті (переместит) заң бар.
x 1 | х 2 = х2 | х1
x 1 ¯ х 2 = х2 ¯ х1
ассоциативті заң бұлар үшін орындалмайды.
x 1 | ( х 2| х3 ) ¹ ( х 1| х2 ) | х3
x 1 ¯ ( х 2¯ х3 ) ¹ ( х 1¯ х2 ) ¯ х3
Және мына заңдар орындалады.

Шеффер мен Веб функциялары бір-бірімен дизьюнкция мен коньюнкцияға арналған Морган заңдары сияқты заңдылықтармен байланысқан.
а) x 1 | х 2 = 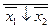 ; в) x 1¯ х 2 =
; в) x 1¯ х 2 = 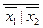
Жалпылама формулалар. &, Ú операциялары ассоциативті болғандықтан 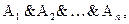
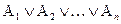 өрнектерінде жақша қоймауға болады. Бірінші өрнек көп мүшелі коньюнкция, екіншісі көпмүшелі дизьюнкция. Бұлар дистрибутивті заңға және Морган заңдарына бағынады:
өрнектерінде жақша қоймауға болады. Бірінші өрнек көп мүшелі коньюнкция, екіншісі көпмүшелі дизьюнкция. Бұлар дистрибутивті заңға және Морган заңдарына бағынады:
Дистрибутивті заң:
(А1 Ù А2 Ù ... Ù Ак ) Ú (В1 Ù В2 Ù ... Ù Вl ) º( А1 Ú В1 ) Ù ( А1 Ú В2) Ù ... Ù( А1 Ú Вl) Ù( А2 Ú В1 ) Ù ( А2 Ú В2) Ù ... Ù( А2 Ú Вl) Ù
... ... ... ...( Ак Ú В1 ) Ù ( Ак Ú В2) Ù ... Ù( Ак Ú Вl) Ù(А1 Ù А2 Ù ... Ù Ак ) Ú (В1 Ù В2 Ù ... Ù Вl ) º
( А1 Ù В1 ) Ú ( А1 Ù В2) Ú ... Ú( А1 Ù Вl)Ú( А2 Ù В1 ) Ú ( А2 Ù В2) Ú ... Ú( А2 Ù Вl) Ú
... ... ...( Ак Ù В1 ) Ú ( Ак Ù В2) Ú ... Ú( Ак Ù Вl) Ú
Көп мушелі коньюнкция мен дизьюнкцияға да Морган заңдарын қолдануға болады.
1. ( 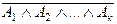 ) º (
) º ( 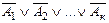 )
)
2. ( 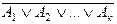 ) º (
) º ( 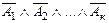 )
)
3. x Ú х Ú ... Ú х= х
4. x Ù х Ù ... Ù х= х
5. x 1 Ú х2Ú ... Ú хn = 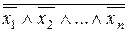
6. x 1 Ù х2Ù ... Ù хn = 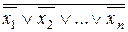
Дата добавления: 2015-08-14; просмотров: 2438;
