Логикалық тұжырымдар формулаларының эквиваленттілігі.
Анықтама. Айталық А мен В бір айнымалылар тізіміне < 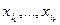 > тәуелді екі формула болсын. Егер олар <
> тәуелді екі формула болсын. Егер олар < 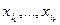 > тізімінің кез- келген бағасында бірдей мәндер қабылдаса оларды эквивалентті формулалар деп атайды.
> тізімінің кез- келген бағасында бірдей мәндер қабылдаса оларды эквивалентті формулалар деп атайды.
Анықтама.Егер F1(x1,x2,…,xn) және F2 (x1,x2,…,xn) формулаларының ақиқаттық кестелері бірдей болса бұл формулалар эквивалентті деп аталады және «~, 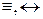 » белгілерінің бірімен көрсетіледі. Екі формуланың эквиваленттілігін білудің стандартты тәсілі екеуінің ақиқаттық кестесін құрып, алынған нәтижені салыстыру болып табылады. Мысалы: (x ® y) ~(
» белгілерінің бірімен көрсетіледі. Екі формуланың эквиваленттілігін білудің стандартты тәсілі екеуінің ақиқаттық кестесін құрып, алынған нәтижені салыстыру болып табылады. Мысалы: (x ® y) ~( 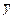 ®
® 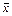 ) формулаларының эквиваленттігін мына ақиқаттық кестеден көруге болады.
) формулаларының эквиваленттігін мына ақиқаттық кестеден көруге болады.
Алынған ақиқаттық кесте әрбір құрама бойынша салыстырылады. Эквивалент формулалардың мынадай қасиеттері бар:
| х | у | x ® y | 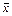
| 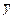
| 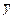 ® ® 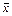
|
Буль алгебрасының негізгі эквивалентті қатынастары (заңдары)
1. Коньюнкция мен дизьюнкцияның ассоциативтілігі
а) x1Ù(x2Ùx3)=(x1Ùx2)Ùx3=x1Ùx2Ùx3; б)x1Ú(x2Úx3)=(x1Úx2)Úx3=x1Úx2Úx3
2. Коньюнкция мен дизьюнкцияның коммутативтілігі
а) x1 &x2=x2 &x1; б)x1 Úx2=x2Úx1
3.Коньюнкцияның дизьюнкцияға қатысты дистрибутивтілігі (Дизьюнкцияның коньюнкцияға қатысты дистрибутивтілігі).
а) x1&(x2Úx3)=(x1&x2)Ú(x1&x3); б) x1Ú(x2 &x3)=(x1Úx2)&(x1Úx3)
4. Идемпотенттілік
а) x & x=х; б) x Úx = х
5. Қос терістеу заңы. 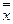 =
= 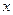
6. 0 мен 1 константаларының қасиеттері:
а) x Ù1=х ; в) x Úx=1; д) 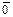 =1;
=1;
б) x Ù0=0 ; г) x Ú0=х ; е) 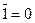 ;
;
7. Морган заңдары:
а) 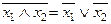 ; б)
; б) 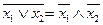
Қарама- қарсылық заңдары:
а) 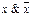 =0 (
=0 ( 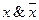 =ж)
=ж)
б) 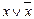 =1 (
=1 ( 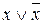 =а)
=а)
Бұл негізгі эквиваленттік қатынастардың ерекшелігі, олар бір –бірінен шықпайды, олардың дұрыстығына, стандартты әдіспен ғана (ақиқат тық кесте) көз жеткізуге болады.
Дата добавления: 2015-08-14; просмотров: 3091;
