I. Расстояние между двумя точками.
Пусть 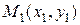 ,
, 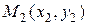 (Рисунок 2.3). Требуется найти
(Рисунок 2.3). Требуется найти 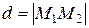 .
.
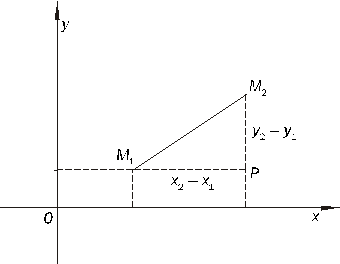
Рисунок 2.3. Расстояние между двумя точками.
Из прямоугольного 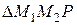 по теореме Пифагора имеем
по теореме Пифагора имеем
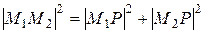 , то есть
, то есть 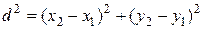 ,
,
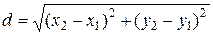 .
.
Эта формула справедлива при любом расположении точек 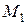 и
и 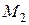 .
.
II. Деление отрезка в данном отношении:
Пусть 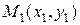 ,
, 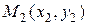 . Требуется найти
. Требуется найти  , лежащую на отрезке
, лежащую на отрезке  и делящую его в данном отношении
и делящую его в данном отношении 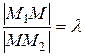 (Рисунок 2.4.).
(Рисунок 2.4.).
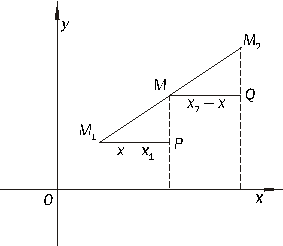
Рисунок 2.4. Деление отрезка в данном отношении.
Из подобия 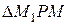 ~
~ 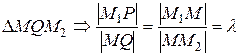 , то есть
, то есть 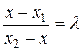 ,
, 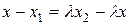 , откуда
, откуда 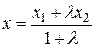 . Аналогично
. Аналогично 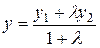 .
.
Таким образом,
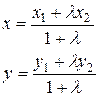 – формула деления отрезка в отношении
– формула деления отрезка в отношении 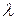 .
.
Если 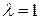 , то
, то
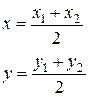 – координаты середины отрезка.
– координаты середины отрезка.
Замечание. Выведенные формулы можно обобщить и на случай пространственной прямоугольной декартовой системы координат. Пусть точки 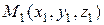 ,
, 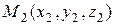 . Тогда
. Тогда
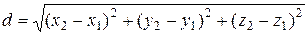 -формуладля нахождениярасстояния между точками
-формуладля нахождениярасстояния между точками 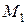 и
и 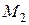 .
.
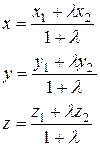 - формула деления отрезка
- формула деления отрезка  в отношении
в отношении  .
.
2.2
Помимо декартовых на плоскости и в пространстве можно построить большое число других систем координат, то есть способов охарактеризовать положение точки на плоскости или в пространстве с помощью двух или трёх числовых параметров (координат). Рассмотрим некоторые из существующих систем координат.
На плоскости можно определить полярную систему координат, которая применяется, в частности, при исследовании вращательных движений.
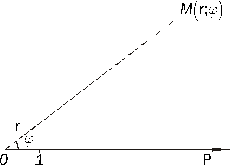
Рисунок 2.5. Полярная система координат.
Зафиксируем на плоскости точку  и выходящую из нее полупрямую
и выходящую из нее полупрямую 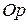 , а также выберем единицу масштаба (Рисунок 2.5). Точка
, а также выберем единицу масштаба (Рисунок 2.5). Точка 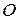 называется полюсом, полупрямая
называется полюсом, полупрямая 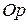 – полярной осью. Произвольной точке
– полярной осью. Произвольной точке 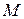 поставим в соответствие два числа
поставим в соответствие два числа 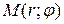 :
:
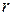 – полярный радиус, равный расстоянию от точки М до полюса О;
– полярный радиус, равный расстоянию от точки М до полюса О;
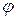 – полярный угол, равный углу между полярной осью
– полярный угол, равный углу между полярной осью 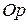 и полупрямой
и полупрямой 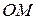 .
.
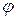 измеряется в радианах, отсчет положительного направления значений
измеряется в радианах, отсчет положительного направления значений 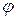 ведется от
ведется от 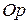 против часовой стрелки, обычно полагают
против часовой стрелки, обычно полагают 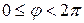 .
.
Полюсу 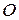 соответствует полярный радиус
соответствует полярный радиус 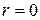 , полярный угол для него не определен.
, полярный угол для него не определен.
Найдем зависимость между прямоугольными и полярными координатами (Рисунок 2.6).
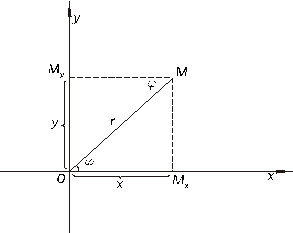
Рисунок 2.6. Связь прямоугольной и полярной систем координат.
Будем считать начало координат  прямоугольной системы координат
прямоугольной системы координат  полюсом, а луч
полюсом, а луч  примем за полярную ось
примем за полярную ось  . Пусть
. Пусть 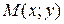 - в прямоугольной декартовой системе координат и
- в прямоугольной декартовой системе координат и 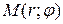 - в полярной системе координат. Найдем зависимость между прямоугольными и полярными координатами.
- в полярной системе координат. Найдем зависимость между прямоугольными и полярными координатами.
Из прямоугольного 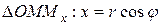 , а из прямоугольного
, а из прямоугольного 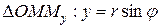 . Таким образом, формулы
. Таким образом, формулы
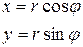 –
–
выражают прямоугольные координаты точки через ее полярные координаты.
Обратную зависимость выражают формулы
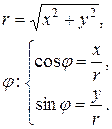
Замечание. Полярный угол можно определить и из формулы 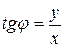 , предварительно определив по прямоугольным координатам, в какой четверти лежит точка.
, предварительно определив по прямоугольным координатам, в какой четверти лежит точка.
Пример 1. Найти полярные координаты точки 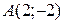 .
.
Решение. Вычисляем 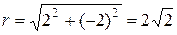 ; полярный угол
; полярный угол 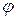 находим из условий:
находим из условий:
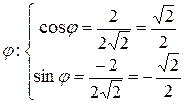 , следовательно,
, следовательно,  , поэтому
, поэтому 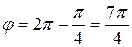 .
.
Имеем 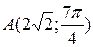 .
.
Пример 2. Найти прямоугольные координаты точки 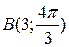 .
.
Решение. Вычисляем
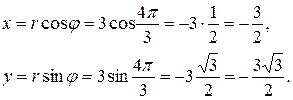
Получаем 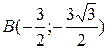 .
.
В трёхмерном пространстве помимо прямоугольной декартовой системы координат часто применяются цилиндрическая и сферическая системы координат.
Цилиндрическая система координат – это полярная система координат в плоскости 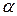 , к которой добавлена пространственная ось
, к которой добавлена пространственная ось 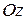 , перпендикулярная данной плоскости (Рисунок 2.7). Положение любой точки
, перпендикулярная данной плоскости (Рисунок 2.7). Положение любой точки 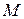 характеризуется тремя числами – её цилиндрическими координатами:
характеризуется тремя числами – её цилиндрическими координатами: 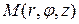 , где
, где 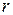 и
и 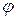 - полярные координаты (полярный радиус и полярный угол) проекции точки
- полярные координаты (полярный радиус и полярный угол) проекции точки 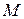 на плоскость, в которой выбрана полярная система координат,
на плоскость, в которой выбрана полярная система координат, 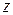 - аппликата, которая равна расстоянию от точки
- аппликата, которая равна расстоянию от точки 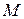 до указанной плоскости.
до указанной плоскости.
Рисунок 2.7. Цилиндрическая система координат
Для установления зависимости между прямоугольной декартовой системой координат и цилиндрической расположим их друг относительно друга как на рисунке 2.8 (плоскость  расположим в плоскости
расположим в плоскости  , причём полярная ось совпадает с положительным направлением оси
, причём полярная ось совпадает с положительным направлением оси 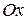 , ось
, ось 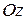 общая в обеих системах координат).
общая в обеих системах координат).
Пусть 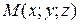 - прямоугольные координаты точки
- прямоугольные координаты точки 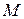 ,
, 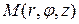 - цилиндрические координаты этой точки,
- цилиндрические координаты этой точки, 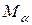 - проекция точки
- проекция точки 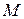 на плоскость
на плоскость 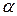 . Тогда
. Тогда
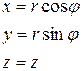 -
-
формулы, связывающие прямоугольные и цилиндрические координаты точки.
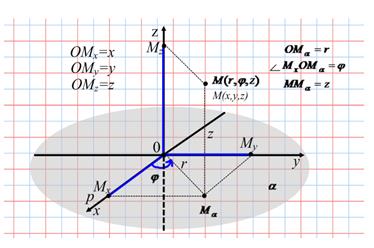
Рисунок 2.8. Зависимость между прямоугольной декартовой
и цилиндрической системами координат
Замечание. Цилиндрические координаты часто применяются при рассмотрении тел вращения, причём ось 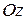 располагается по оси вращения.
располагается по оси вращения.
Сферическая система координат может быть построена следующим образом. Выберем в плоскости 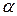 полярную ось
полярную ось 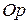 . Через точку
. Через точку 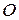 проведём прямую перпендикулярную плоскости
проведём прямую перпендикулярную плоскости 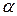 (нормаль). Тогда любой точке пространства
(нормаль). Тогда любой точке пространства 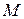 можно поставить в соответствие три действительных числа
можно поставить в соответствие три действительных числа 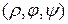 , где
, где 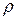 - расстояние от точки
- расстояние от точки 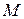 до
до 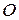 ,
, 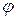 - угол между осью
- угол между осью 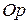 и проекцией отрезка
и проекцией отрезка 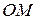 на плоскость
на плоскость 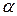 ,
, 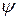 - угол между нормалью и отрезком
- угол между нормалью и отрезком 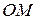 . Заметим, что
. Заметим, что 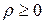 ,
, 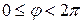 ,
, 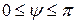 .
.
Если расположить плоскость 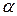 в плоскости
в плоскости 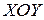 , причём полярную ось выбрать совпадающей с положительным направлением оси
, причём полярную ось выбрать совпадающей с положительным направлением оси 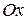 , в качестве нормали выбрать ось
, в качестве нормали выбрать ось  (Рисунок 2.9), то получаем формулы связывающие эти две системы координат
(Рисунок 2.9), то получаем формулы связывающие эти две системы координат
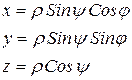 .
.
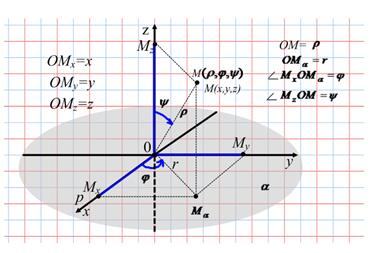
Рисунок 2.9. Связь между сферической и прямоугольной декартовой
системами координат
2.3
Скалярные величины, или скаляры полностью характеризуются своим численным значением в выбранной системе единиц. Векторные величины или векторы кроме численного значения обладают также направлением. Например, если мы скажем, что дует ветер со скоростью 10 м/сек, то тем самым введем скалярную величину скорости ветра, но если мы скажем, что дует юго-западный ветер со скоростью 10 м/сек, то в этом случае скорость ветра будет уже вектором.
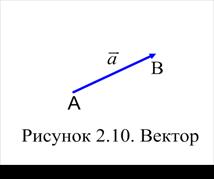
Вектором называется направленный отрезок, имеющий определенную длину, т.е. отрезок определенной длины, у которого одна из ограничивающих точек принимается за начало, а вторая - за конец. Вектор будем обозначать либо  , либо
, либо  (Рисунок 2.10).
(Рисунок 2.10).
 Длина вектора обозначается символом
Длина вектора обозначается символом 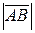 или
или 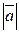 и называется модулем вектора. Вектор, у которого длина равна 1, называется единичным. Вектор называется нулевым, если начало и конец его совпадают, и обозначается θ или
и называется модулем вектора. Вектор, у которого длина равна 1, называется единичным. Вектор называется нулевым, если начало и конец его совпадают, и обозначается θ или 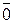 . Нулевой вектор не имеет определенного направления и имеет длину, равную нулю. Векторы
. Нулевой вектор не имеет определенного направления и имеет длину, равную нулю. Векторы  и
и  , расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Два вектора
, расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Два вектора  и
и  называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными.
называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление. Все нулевые векторы считаются равными.
Два коллинеарных вектора, отличные от нулевых, имеющие равные модули, но противоположное направление, называются противоположными. Вектор, противоположный  , обозначается
, обозначается 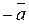 , для
, для 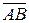 противоположный вектор
противоположный вектор 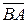 .
.
К числу линейных операций над векторами относят операции сложения, вычитания векторов и умножения вектора на число, т.е. операции, результатом которых является вектор.
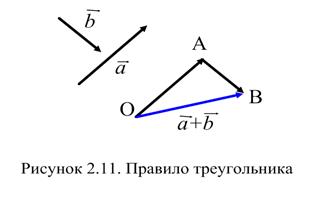 Определим указанные операции над векторами. Пусть даны два вектора
Определим указанные операции над векторами. Пусть даны два вектора  и
и  . Возьмем произвольную точку О и построим вектор
. Возьмем произвольную точку О и построим вектор 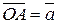 , от точки А отложим вектор
, от точки А отложим вектор 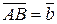 . Тогда вектор
. Тогда вектор 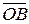 , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается
, соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается 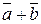 . Рассмотренное правило нахождения суммы векторов носит название правила треугольников (Рисунок 2.11).
. Рассмотренное правило нахождения суммы векторов носит название правила треугольников (Рисунок 2.11).
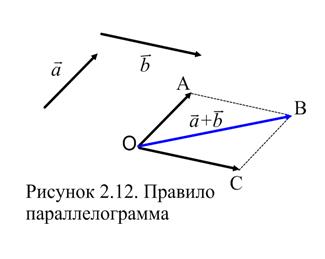 Ту же самую сумму векторов можно получить и иным способом (Рисунок 2.12). Отложим от точки
Ту же самую сумму векторов можно получить и иным способом (Рисунок 2.12). Отложим от точки  вектор
вектор  и вектор
и вектор  . Построим на этих векторах как на сторонах параллелограмм
. Построим на этих векторах как на сторонах параллелограмм  . Вектор
. Вектор 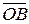 , являющийся диагональю параллелограмма, проведенной из вершины
, являющийся диагональю параллелограмма, проведенной из вершины  , и будет суммой
, и будет суммой 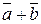 . Это правило нахождения суммы носит название правила параллелограмма.
. Это правило нахождения суммы носит название правила параллелограмма.
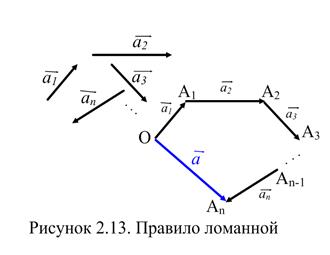 Сумму любого конечного числа векторов можно получить по правилу ломанной (Рисунок 2.13). Из произвольной точки
Сумму любого конечного числа векторов можно получить по правилу ломанной (Рисунок 2.13). Из произвольной точки  откладываем вектор
откладываем вектор  , далее откладываем вектор
, далее откладываем вектор  и т.д. Вектор, соединяющий начало первого с концом последнего, является суммой
и т.д. Вектор, соединяющий начало первого с концом последнего, является суммой
| |
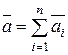 . Очевидно, если конец последнего слагаемого вектора совпадает с началом первого, то сумма векторов равна нуль-вектору.
. Очевидно, если конец последнего слагаемого вектора совпадает с началом первого, то сумма векторов равна нуль-вектору.
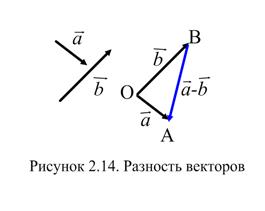 Разностью двух векторов
Разностью двух векторов  и
и  называется такой вектор
называется такой вектор  , сумма которого с вычитаемым вектором
, сумма которого с вычитаемым вектором  дает вектор
дает вектор  . Отсюда правило построения вектора-разности (Рисунок 2.14). Из точки
. Отсюда правило построения вектора-разности (Рисунок 2.14). Из точки  откладываем вектор
откладываем вектор 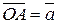 и вектор
и вектор 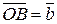 . Вектор
. Вектор 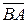 , соединяющий концы уменьшаемого вектора
, соединяющий концы уменьшаемого вектора  и вычитаемого вектора
и вычитаемого вектора  и направленный от вычитаемого к уменьшаемому вектору, является разностью
и направленный от вычитаемого к уменьшаемому вектору, является разностью 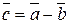 .
.
Произведением вектора  на действительное число λ называется вектор
на действительное число λ называется вектор 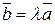 , который коллинеарен вектору
, который коллинеарен вектору  , имеет длину
, имеет длину 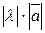 и то же направление, что и вектор
и то же направление, что и вектор  , если
, если  , и направление, противоположное вектору
, и направление, противоположное вектору  , если
, если 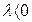 .
.
Введенные линейные операции над векторами обладают свойствами:
10. Коммутативность сложения: 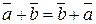 .
.
20. Ассоциативность сложения: 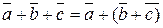 .
.
30. Существование нейтрального элемента по сложению: 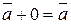 .
.
40. Существование противоположного элемента по сложению:
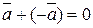 .
.
50. Дистрибутивность умножения на число относительно сложения векторов: 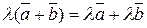 .
.
60. Дистрибутивность умножения вектора на сумму двух чисел:
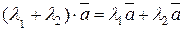 .
.
70. Свойство ассоциативности относительно умножения вектора на произведение чисел:  .
.
2.4
Пусть дана система векторов:
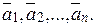 (2.1)
(2.1)
Выражение 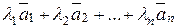 , где λi (i = 1,2,…, n) - некоторые числа, называется линейной комбинацией системы векторов (2.1). Система векторов (2.1) называется линейно зависимой, если их линейная комбинация равна нулю при условии, что не все числа λ1, λ2, …, λn равны нулю. Система векторов (2.1) называется линейно независимой, если их линейная комбинация равна нулю только при условии, что все числа λi = 0 (
, где λi (i = 1,2,…, n) - некоторые числа, называется линейной комбинацией системы векторов (2.1). Система векторов (2.1) называется линейно зависимой, если их линейная комбинация равна нулю при условии, что не все числа λ1, λ2, …, λn равны нулю. Система векторов (2.1) называется линейно независимой, если их линейная комбинация равна нулю только при условии, что все числа λi = 0 ( 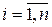 ). Можно дать другое определение линейной зависимости векторов. Система векторов (2.1) называется линейно зависимой, если какой-либо вектор этой системы линейно выражается через остальные, в противном случае система векторов (2.1) линейно независима.
). Можно дать другое определение линейной зависимости векторов. Система векторов (2.1) называется линейно зависимой, если какой-либо вектор этой системы линейно выражается через остальные, в противном случае система векторов (2.1) линейно независима.
Для векторов, лежащих в плоскости, справедливы следующие утверждения.
10. Всякие три вектора на плоскости линейно зависимы.
20. Если число данных векторов на плоскости больше трех, то они также линейно зависимы.
30. Для того, чтобы два вектора на плоскости были линейно независимы, необходимо и достаточно, чтобы они были неколлинеарны.
Таким образом, максимальное число линейно независимых векторов на плоскости равно двум.
Векторы называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости. Для векторов пространства справедливы следующие утверждения.
10. Всякие четыре вектора пространства линейно зависимы.
20. Если число данных векторов в пространстве больше четырех, то они также линейно зависимы.
30. Для того, чтобы три вектора были линейно независимы, необходимо и достаточно, чтобы они были некомпланарны.
Таким образом, максимальное число линейно независимых векторов в пространстве равно трем.
Всякая максимальная подсистема линейно независимых векторов, через которую выражается любой вектор этой системы, называется базисомрассматриваемой системы векторов. Несложно заключить, что базис на плоскости состоит из двух неколлинеарных векторов, а базис в пространстве состоит из трех некомпланарных векторов. Число векторов базиса называется рангом системы векторов. Коэффициенты разложения вектора по векторам базиса называют координатами вектора в данном базисе.
Пусть векторы 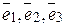 образуют базис и пусть
образуют базис и пусть  , тогда числа λ1, λ2, λ3– координаты вектора
, тогда числа λ1, λ2, λ3– координаты вектора  в базисе
в базисе 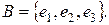 В этом случае записывают
В этом случае записывают 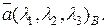 Можно показать, что разложение вектора по базису является единственным. Основное значение базиса состоит в том, что линейные операции над векторами становятся обычными линейными операциями над числами – координатами этих векторов. С помощью свойств линейных операций над векторами можно доказать следующую теорему.
Можно показать, что разложение вектора по базису является единственным. Основное значение базиса состоит в том, что линейные операции над векторами становятся обычными линейными операциями над числами – координатами этих векторов. С помощью свойств линейных операций над векторами можно доказать следующую теорему.
Теорема. При сложении двух векторов их соответствующие координаты складываются. При умножении вектора на число все его координаты умножаются на это число.
Таким образом, если 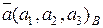 и
и 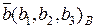 , то
, то 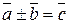 , где
, где 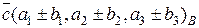 , и
, и 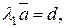 где
где 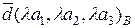 , λ – некоторое число.
, λ – некоторое число.
Обычно множество всех векторов на плоскости, приведенных к общему началу, с введенными линейными операциями обозначают V2, а множество всех векторов пространства, приведенных к общему началу, обозначают V3. Множества V2 и V3 называют пространствами геометрических векторов.
2.5
Углом между векторами  и
и  называется наименьший угол
называется наименьший угол 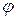 (
( 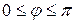 ), на который надо повернуть один из векторов до его совпадения со вторым после приведения этих векторов к общему началу.
), на который надо повернуть один из векторов до его совпадения со вторым после приведения этих векторов к общему началу.
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними. Скалярное произведение векторов  и
и  обозначают
обозначают 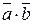 , или
, или 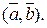
Если угол между векторами  и
и  равен
равен 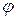 , то
, то
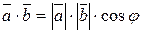 . (2.2)
. (2.2)
С геометрической точки зрения скалярное произведение векторов равно произведению модуля одного вектора на проекцию на него другого вектора. Из равенства (2.2) следует, что
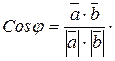 (2.3)
(2.3)
Отсюда условие ортогональности двух векторов: два вектора  и
и  ортогональны тогда и только тогда, когда их скалярное произведение равно нулю, т.е.
ортогональны тогда и только тогда, когда их скалярное произведение равно нулю, т.е. 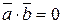 .
.
Скалярное произведение векторов не является линейной операцией, так как ее результатом является число, а не вектор.
Свойства скалярного произведения.
1º. 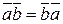 – коммутативность.
– коммутативность.
2º. 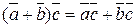 – дистрибутивность.
– дистрибутивность.
3º. 
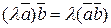 – ассоциативность относительно числового множителя.
– ассоциативность относительно числового множителя.
4º. 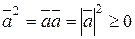 - свойство скалярного квадрата.
- свойство скалярного квадрата.
Из свойства 4º следует определение длины вектора:
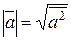 . (2.4)
. (2.4)
Пусть в пространстве V3 задан базис 
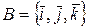 , где векторы
, где векторы  – единичные векторы (их называют ортами), направление каждого их которых совпадает с положительным направлением координатных осей Ох, Oy, Oz прямоугольной декартовой системы координат.
– единичные векторы (их называют ортами), направление каждого их которых совпадает с положительным направлением координатных осей Ох, Oy, Oz прямоугольной декартовой системы координат.
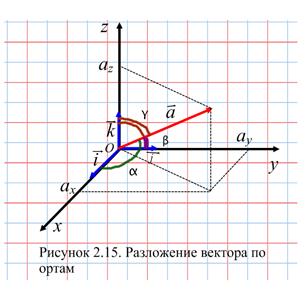
Разложим вектор  пространства V3 по этому базису (Рисунок 2.15):
пространства V3 по этому базису (Рисунок 2.15):
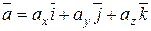 . (2.5)
. (2.5)
Векторы 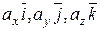 называют составляющими вектора
называют составляющими вектора  по осям координат, или компонентами, числа ax, ay, az – прямоугольные декартовы координаты вектора а. Направление вектора
по осям координат, или компонентами, числа ax, ay, az – прямоугольные декартовы координаты вектора а. Направление вектора  определяется углами α, β, γ, образованными им с координатными прямыми. Косинус этих углов называют направляющими вектора
определяется углами α, β, γ, образованными им с координатными прямыми. Косинус этих углов называют направляющими вектора  . Тогда направляющие косинусы определяются по формулам:
. Тогда направляющие косинусы определяются по формулам:
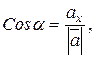
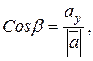
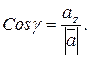
Несложно показать, что 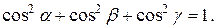
Выразим скалярное произведение в координатной форме.
Пусть 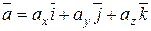 и
и 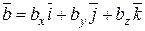 . Перемножая эти векторы как многочлены и учитывая, что
. Перемножая эти векторы как многочлены и учитывая, что 
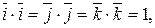 получим выражение для нахождения скалярного произведения в координатной форме:
получим выражение для нахождения скалярного произведения в координатной форме:
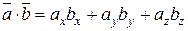 , (2.6)
, (2.6)
т.е. скалярное произведение двух векторов равно сумме парных произведений одноименных координат.
Из (2.6) и (2.4) следует формула для нахождения длины вектора  :
:
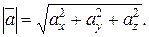 (2.7)
(2.7)
Из (2.6) и (2.7) получаем формулу для определения угла между векторами:
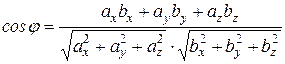 . (2.8)
. (2.8)
2.6
Тройка векторов называется упорядоченной, если указано, какой из них считается первым, какой – вторым, а какой третьим.
Упорядоченная тройка векторов называется правой, если после приведения их к общему началу из конца третьего вектора кратчайший поворот от первого ко второму вектору совершается против часовой стрелки. В противном случае тройка векторов называется левой. Например, на рисунке 2.15 векторы 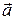 ,
, 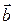 ,
, 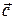 образуют правую тройку векторов, а векторы
образуют правую тройку векторов, а векторы 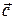 ,
, 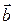 ,
, 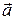 - левую тройку векторов.
- левую тройку векторов.
Аналогичным образом вводится понятие правой и левой систем координат в трехмерном пространстве.
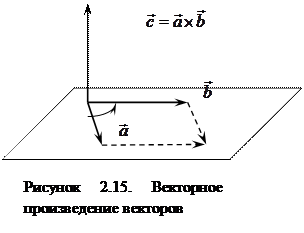
Векторным произведением вектора 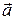 на вектор
на вектор 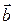 называется вектор
называется вектор 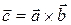 (другое обозначение
(другое обозначение 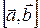 ), который:
), который:
1) имеет длину 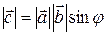 , где
, где 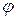 – угол между векторами
– угол между векторами 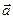 и
и 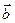 ;
;
2) перпендикулярен векторам 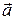 и
и 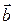 (
( 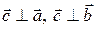 ), т.е. перпендикулярен плоскости, в которой лежат векторы
), т.е. перпендикулярен плоскости, в которой лежат векторы 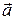 и
и 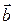 ;
;
3) направлен так, что векторы 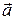 ,
, 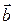 ,
, 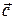 образуют правую тройку векторов (Рисунок 2.15).
образуют правую тройку векторов (Рисунок 2.15).
По определению найдём векторное произведение координатных ортов 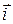 ,
, 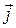 ,
, 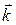 :
:
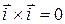 ,
, 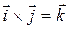 ,
, 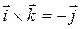
 ,
, 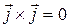 ,
, 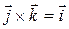
 ,
, 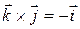 ,
, 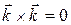
Если 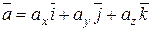 ,
, 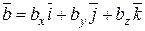 , то координаты векторного произведения вектора
, то координаты векторного произведения вектора 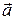 на вектор
на вектор 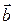 определяются по формуле:
определяются по формуле:
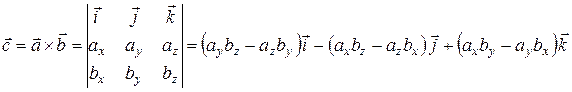 .
.
Из определения следует геометрический смысл векторного произведения: модуль вектора 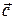 равен площади параллелограмма, построенного на векторах
равен площади параллелограмма, построенного на векторах 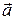 и
и 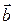 .
.
Свойства векторного произведения:
10. 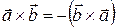 .
.
20. 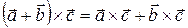 .
.
30. 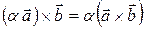 .
.
40. 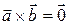 , если векторы
, если векторы 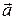 и
и 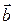 коллинеарны, или один из этих векторов нулевой.
коллинеарны, или один из этих векторов нулевой.
Пример 3. Параллелограмм построен на векторах 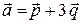 и
и 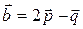 , где
, где 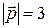 ,
, 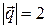 ,
, 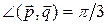 . Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.
. Вычислить длину диагоналей этого параллелограмма, угол между диагоналями и площадь параллелограмма.
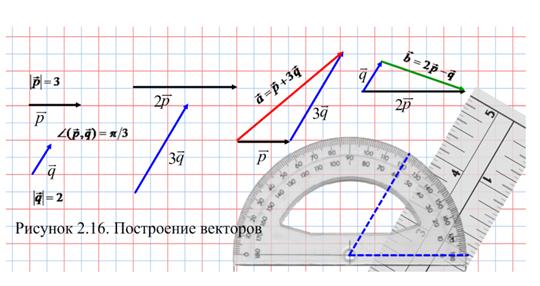
Решение. Построение векторов 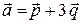 и
и 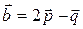 показано на рисунке 2.16, построение параллелограмма на этих векторах показано на рисунке 2.17.
показано на рисунке 2.16, построение параллелограмма на этих векторах показано на рисунке 2.17.
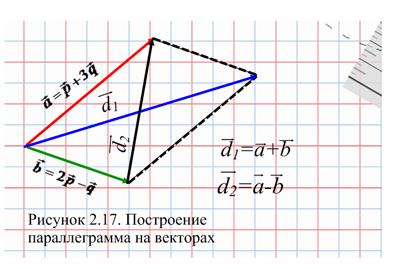
Проведём аналитическое решение этой задачи. Выразим вектора, определяющие диагонали построенного параллелограмма, через векторы 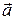 и
и 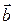 , а затем через
, а затем через 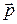 и
и 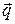 . Находим
. Находим 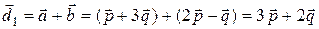 ,
, 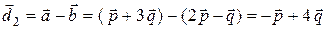 . Далее находим длины диагоналей параллелограмма, как длины построенных векторов
. Далее находим длины диагоналей параллелограмма, как длины построенных векторов
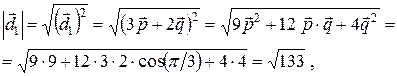
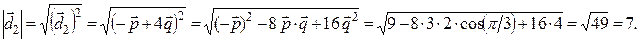
Угол между диагоналями параллелограмма обозначим через 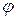 . Тогда из формулы скалярного произведения векторов имеем:
. Тогда из формулы скалярного произведения векторов имеем:
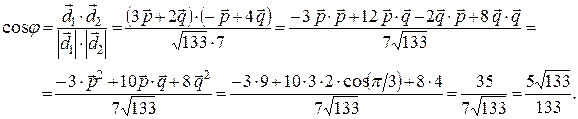
Следовательно, 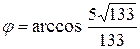 .
.
Используя свойства векторного произведения, вычислим площадь параллелограмма:
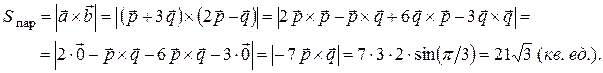
2.7
Пусть даны три вектора  ,
,  и
и 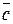 . Представим себе, что вектор
. Представим себе, что вектор  умножается векторно на
умножается векторно на  и вектор
и вектор 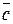 и полученный вектор
и полученный вектор  умножается скалярно на вектор
умножается скалярно на вектор 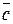 , тем самым определяется число
, тем самым определяется число 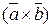
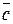 . Оно называется векторно-скалярным или смешанным произведением трёх векторов
. Оно называется векторно-скалярным или смешанным произведением трёх векторов  ,
,  и
и 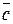 . Обозначается
. Обозначается 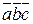 или
или 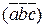 .
.
Выясним геометрический смысл смешанного произведения 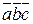 (Рисунок 2.18). Пусть
(Рисунок 2.18). Пусть  ,
,  ,
, 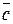 не компланарны. Построим на этих векторах параллелепипед как на ребрах. Векторное произведение
не компланарны. Построим на этих векторах параллелепипед как на ребрах. Векторное произведение  есть вектор
есть вектор 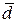 , модуль которого равен площади параллелограмма (основание параллелепипеда), построенного на векторах
, модуль которого равен площади параллелограмма (основание параллелепипеда), построенного на векторах  и
и  и направлен
и направлен  перпендикулярно к плоскости параллелограмма.
перпендикулярно к плоскости параллелограмма.
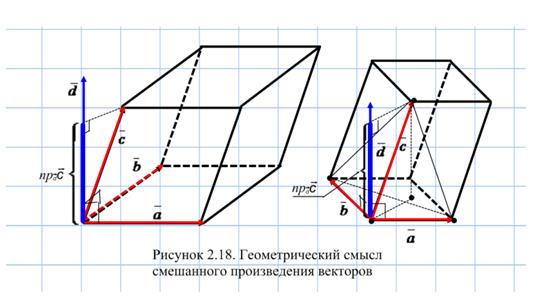
Скалярное произведение 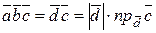 (равно произведению модуля вектора
(равно произведению модуля вектора  и проекции
и проекции 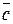 на
на  ). Высота построенного параллелепипеда есть абсолютная величина этой проекции. Следовательно, абсолютная величина смешанного произведения трёх векторов равна объёму параллелепипеда, построенного на векторах
). Высота построенного параллелепипеда есть абсолютная величина этой проекции. Следовательно, абсолютная величина смешанного произведения трёх векторов равна объёму параллелепипеда, построенного на векторах  ,
,  и
и 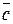 , т.е.
, т.е. 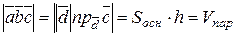 .
.
Отсюда объем треугольной пирамиды 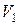 , построенной на векторах
, построенной на векторах  ,
,  и
и 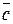 , вычисляется по формуле
, вычисляется по формуле 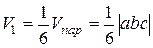 .
.
Отметим ещё некоторые свойства смешанного произведения векторов.
1о. Знак произведения 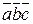 положителен, если векторы
положителен, если векторы  ,
,  ,
, 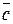 образуют систему, одноименную с основной, и отрицателен в противном случае.
образуют систему, одноименную с основной, и отрицателен в противном случае.
Действительно, скалярное произведение 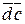 положительно, если угол между
положительно, если угол между  и
и 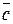 острый и отрицательно, если угол тупой. При остром угле между
острый и отрицательно, если угол тупой. При остром угле между  и
и 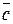 векторы
векторы 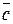 и
и  расположены по одну сторону относительно основания параллелепипеда, и следовательно, из конца вектора
расположены по одну сторону относительно основания параллелепипеда, и следовательно, из конца вектора 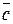 вращение от
вращение от  к
к  будет видно так же, как из конца вектора
будет видно так же, как из конца вектора  , т.е. в положительном направлении (против часовой стрелки).
, т.е. в положительном направлении (против часовой стрелки).
При тупом угле  и
и 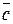 векторы
векторы 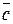 и
и  расположены по разные стороны относительно плоскости параллелограмма, лежащего в основании параллелепипеда, и следовательно, из конца вектора
расположены по разные стороны относительно плоскости параллелограмма, лежащего в основании параллелепипеда, и следовательно, из конца вектора 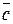 вращение от
вращение от  к
к  видно в отрицательном направлении (по часовой стрелке).
видно в отрицательном направлении (по часовой стрелке).
2о Смешанное произведение не меняется при круговой перестановке его сомножителей: 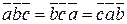 .
.
3о При перестановке любых двух векторов смешанное произведение изменяет только знак. Например, 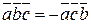 ,
, 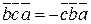 .
.
4о Необходимым и достаточным условием компланарности 3-х векторов служит условие равенства нулю их смешанного произведения: 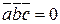 .
.
Действительно, это свойство следует из геометрического смысла смешанного произведения. В этом случае параллелепипед вырождается в часть плоскости, т.е. имеет нулевой объем.
5о Пусть векторы  ,
,  ,
, 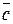 заданы их разложениями по ортам:
заданы их разложениями по ортам:
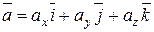 ,
, 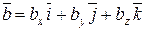 ,
, 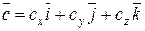 ,
,
тогда  .
.
Действительно,
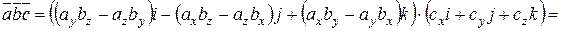
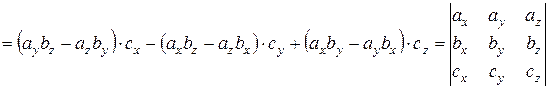 .
.
6о Для того чтобы три вектора  ,
,  ,
, 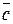 были компланарны (векторы заданы разложением по ортам как в предыдущем свойстве) необходимо и достаточно, чтобы определитель
были компланарны (векторы заданы разложением по ортам как в предыдущем свойстве) необходимо и достаточно, чтобы определитель
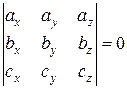 .
.
7о 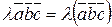 .
.
8о 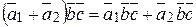 .
.
Пример 4. Проверить, компланарны ли векторы  ,
, 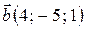 ,
, 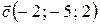 ? Если векторы некомпланарны, то найти объём параллелепипеда, построенного на этих векторах.
? Если векторы некомпланарны, то найти объём параллелепипеда, построенного на этих векторах.
Решение. Если векторы компланарны, то их смешанное произведение равно нулю. Найдем смешанное произведение данных векторов, вычислив определитель:
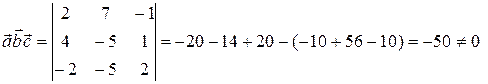 векторы
векторы  ,
,  ,
, 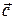 некомпланарны. Тогда
некомпланарны. Тогда 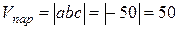 .
.
Лекция 3.Системы линейных уравнений и методы их решения.
План лекции
3.1. Системы линейных уравнений. Основные определения.
3.2. Метод Гаусса решения систем линейных уравнений.
3.3. Критерий совместности систем линейных уравнений.
3.4. Метод Крамера решения систем линейных уравнений.
3.5. Обратная матрица. Методы её нахождения.
3.6. Матричный метод решения систем линейных уравнений.
3.7. Однородная система линейных уравнений, условие существования ненулевых решений.
3.1
Системой 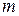 линейных уравнений с
линейных уравнений с 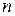 неизвестными называются соотношения вида
неизвестными называются соотношения вида
 (3.1)
(3.1)
где 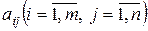 - коэффициенты системы,
- коэффициенты системы, 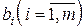 - свободные члены,
- свободные члены, 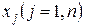 - неизвестные системы.
- неизвестные системы.
Система (3.1) называется однородной, если все свободные члены 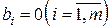 . Система (3.1) называется неоднородной, если хотя бы один из свободных членов
. Система (3.1) называется неоднородной, если хотя бы один из свободных членов  .
.
Решением системы называется совокупность чисел 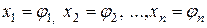 , при подстановке которых в уравнения системы вместо соответствующих неизвестных каждое уравнение системы превращается в тождество. Система, не имеющая ни одного решения, называется несовместной, или противоречивой. Система, имеющая хотя бы одно решение, называется совместной.
, при подстановке которых в уравнения системы вместо соответствующих неизвестных каждое уравнение системы превращается в тождество. Система, не имеющая ни одного решения, называется несовместной, или противоречивой. Система, имеющая хотя бы одно решение, называется совместной.
Совместная система называется определенной, если она имеет единственное решение. Если совместная система имеет более одного решения, то она называется неопределенной. Однородная система всегда совместна, так как имеет, по крайней мере, нулевое решение 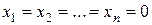 . Выражение для неизвестных
. Выражение для неизвестных 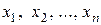 , из которого можно получить любое конкретное решение системы, называют ее общим решением, а любое конкретное решение системы – ее частным решением. Две системы с одними и теми же неизвестными эквивалентны (равносильны), если каждое решение одной из них является решением другой или обе системы несовместны.
, из которого можно получить любое конкретное решение системы, называют ее общим решением, а любое конкретное решение системы – ее частным решением. Две системы с одними и теми же неизвестными эквивалентны (равносильны), если каждое решение одной из них является решением другой или обе системы несовместны.
Рассмотрим методы решения систем линейных уравнений.
3.2
Одним из основных методов решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Суть этого метода состоит в сведении системы линейных уравнений к ступенчатому виду. При этом над уравнениями приходится проводить следующие элементарные преобразования:
1. Перестановка уравнений системы.
2. Прибавление к одному уравнению другого уравнения.
3. Умножение обеих частей уравнения на число, отличное от нуля.
4. Прибавление к одному уравнению другого, умноженного на некоторое число, отличное от нуля.
5. Вычеркивание уравнений вида 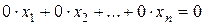 , т.е. тождеств
, т.е. тождеств 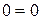 .
.
В результате элементарных преобразований система преобразуется в эквивалентную ей систему.
Рассмотрим алгоритм метода Гаусса. Пусть дана система вида (3.1). Предположим, что в этой системе коэффициент 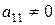 . Заметим, что этого всегда можно достигнуть перестановкой уравнений системы. Для исключения неизвестной
. Заметим, что этого всегда можно достигнуть перестановкой уравнений системы. Для исключения неизвестной 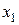 во всех уравнениях, начиная со второго, умножим первое уравнение системы последовательно на числа
во всех уравнениях, начиная со второго, умножим первое уравнение системы последовательно на числа 
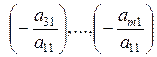 и добавим соответственно ко 2-му, 3-му, ...,
и добавим соответственно ко 2-му, 3-му, ..., 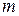 - му уравнению системы.
- му уравнению системы.
В результате система примет вид:

Продолжая этот процесс дальше, исключим неизвестную 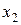 из всех уравнений, начиная с третьего. Для этого умножим второе уравнение на числа
из всех уравнений, начиная с третьего. Для этого умножим второе уравнение на числа 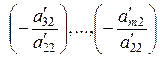 и добавим к 3-му, ..., к
и добавим к 3-му, ..., к 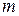 - му уравнению системы. Следующие шаги метода Гаусса осуществляются аналогично. Если в результате преобразований получится тождественное уравнение, то вычеркнем его из системы. Если на некотором шаге метода Гаусса получается уравнение вида:
- му уравнению системы. Следующие шаги метода Гаусса осуществляются аналогично. Если в результате преобразований получится тождественное уравнение, то вычеркнем его из системы. Если на некотором шаге метода Гаусса получается уравнение вида:
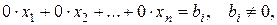 (3.2)
(3.2)
тогда рассматриваемая система несовместна и дальнейшее ее решение прекращается. Если же уравнение вида (3.2) не встретится при выполнении элементарных преобразований, то не более чем через 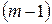 - шагов система (3.1) будет преобразована к ступенчатому виду:
- шагов система (3.1) будет преобразована к ступенчатому виду:
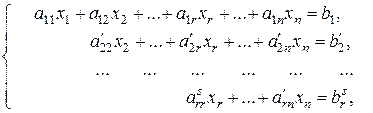 (3.3)
(3.3)
где 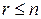 . Если
. Если  , то говорят, что система свелась к треугольному виду. В этом случае система имеет единственное решение, которое находим, решая систему снизу вверх.
, то говорят, что система свелась к треугольному виду. В этом случае система имеет единственное решение, которое находим, решая систему снизу вверх.
Если 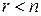 , то говорят, что система свелась к трапециидальному виду. В этом случае система является неопределенной. Для нахождения общего решения системы в этом случае выбирают
, то говорят, что система свелась к трапециидальному виду. В этом случае система является неопределенной. Для нахождения общего решения системы в этом случае выбирают 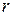 главных и
главных и 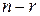 свободных неизвестных. Например, неизвестные
свободных неизвестных. Например, неизвестные 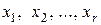 принимают за главные, а неизвестные
принимают за главные, а неизвестные 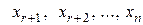 принимают за свободные. Переносим свободные неизвестные в правую часть уравнений и выражаем главные неизвестные через свободные. В результате получаем общее решение системы:
принимают за свободные. Переносим свободные неизвестные в правую часть уравнений и выражаем главные неизвестные через свободные. В результате получаем общее решение системы:
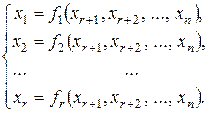 (3.4)
(3.4)
Для получения частного решения системы необходимо будет в (3.4) придать свободным переменным конкретные значения.
Заметим, что так как в методе Гаусса все преобразования выполняются над коэффициентами при неизвестных уравнений и свободными членами, то на практике обычно этот метод применяют к матрице, составленной из коэффициентов при неизвестных и столбца свободных членов. Эту матрицу называют расширенной. С помощью элементарных преобразований эту матрицу сводят к ступенчатому виду. После чего по полученной матрице восстанавливают систему и применяют к ней все предыдущие рассуждения.
Пример 1. Решить систему:
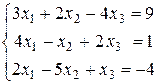 .
.
Решение. Составляем расширенную матрицу и сводим ее к ступенчатому виду:
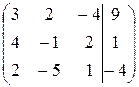 ~*)
~*)  ~**)
~**) 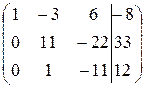 ~ ***)
~ ***)
~ 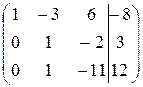 ~****)
~****) 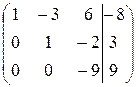 .
.
*) – первую строку умножили на 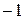 и добавили ко второй, полученную строку записали на первое место (цель этого преобразования получить единицу в первом столбце); оставили без изменения вторую строку на втором месте (можно было сюда записать первоначальную первую строку) и третью строку на своём месте.
и добавили ко второй, полученную строку записали на первое место (цель этого преобразования получить единицу в первом столбце); оставили без изменения вторую строку на втором месте (можно было сюда записать первоначальную первую строку) и третью строку на своём месте.
**) – умножили первую строку на 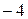 и на
и на 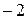 и добавили ко второй и третьей соответственно.
и добавили ко второй и третьей соответственно.
***) – вторую строку умножили на 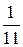 .
.
****) – вторую строку умножили на 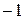 и добавили к третьей.
и добавили к третьей.
Матрица свелась к треугольному виду, следовательно, система имеет единственное решение.
Восстанавливаем систему и решаем её снизу вверх.
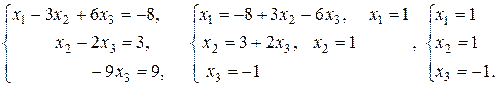
Пример 2. Решить систему:
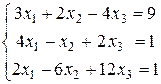 .
.
Решение. Составляем расширенную матрицу и сводим её к ступенчатому виду:
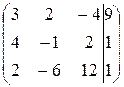 ~
~ 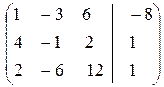 ~
~ 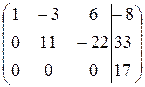 .
.
Заметим, что выполнялись преобразования те же, что и в примере 1.
Данная система не совместна, так как последняя строка матрицы соответствует уравнению 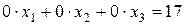 , которое решения не имеет.
, которое решения не имеет.
Пример 3. Решить систему:
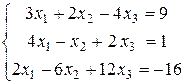
Решение. Составляем расширенную матрицу и сводим ее к ступенчатому виду:
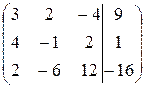 ~
~  ~
~ 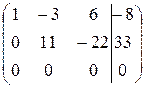 ~*)
~*)
~ 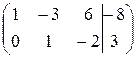 .
.
*) - вторую строку умножили на 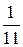 и вычеркнули третью строку.
и вычеркнули третью строку.
Дата добавления: 2015-08-21; просмотров: 10320;
