Лекция 2. Системы координат. Скалярные и векторные величины.

План лекции

2.1. Прямоугольные декартовы координаты на плоскости и в пространстве. Основные задачи на прямоугольные координаты.

2.2. Полярная система координат, ее связь с прямоугольной. Цилиндрическая и сферическая системы координат.

2.3. Скаляры и векторы, основные определения. Линейные действия над векторами.

2.4. Линейная зависимость системы векторов, базис и ранг системы векторов, координаты вектора.

2.5. Скалярное произведение двух векторов, длина вектора, угол между векторами, условие ортогональности.

2.6. Векторное произведение векторов, его приложения.

2.7. Смешанное произведение векторов, его приложения.

2.1

Одним из важных вопросов математики является определение положения точки.

Координатной прямой называется прямая, на которой выбрано начало отсчета, положительное направление и единица масштаба.

Как известно, между точками координатной (числовой) прямой и множеством действительных чисел существует взаимно-однозначное соответствие. Поэтому положение точки на прямой полностью определяется одним числом – координатой точки. Для определения положения точки на плоскости необходимо ввести систему координат на плоскости. Это можно сделать многими способами, один из которых – построение прямоугольной декартовой системы координат.

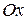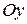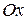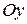Возьмем на плоскости две взаимно перпендикулярные прямые и с указанными на них положительными направлениями и единицей масштаба (рисунок 2.1). Прямые и называются координатными осями, причем 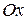- ось абсцисс, 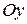- ось ординат, точка их пересечения называется началом координат. Координатные ос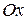и и 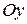с выбранной единицей масштаба называются прямоугольной декартовой системой координат на плоскости. Произвольной точке 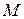плоскости поставим в соответствие два числа:

абсциссу 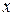, равную расстоянию от точки 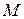до оси 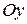, взятому со знаком «+», если 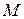лежит правее 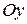, и со знаком «-», если 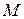лежит левее ;

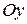ординату , равную расстоянию от точки 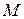до оси 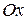, взятому со знаком «+», если 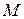лежит выше 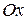, и со знаком «-», если 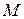лежит ниже .

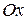Абсцисса 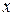и ордината называются прямоугольными декартовыми координатами точки 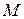. Записывают .

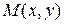Между точками плоскости и упорядоченными парами чисел 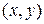- их координатами существует взаимно-однозначное соответствие: каждой точке плоскости соответствует единственная пара действительных чисел 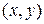и, обратно, каждой паре действительных чисел 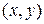соответствует единственная точка плоскости.

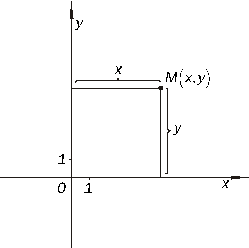
Рисунок 2.1. Прямоугольная система координат на плоскости.

Аналогичным образом вводим понятие прямоугольной декартовой системы координат в пространстве.

Возьмем в трёхмерном пространстве три взаимно перпендикулярные прямые 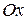, , 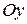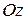с общим началом, укажем на них положительные направления и единицу масштаба. Такая система называется прямоугольной декартовой системой координат в пространстве (Рисунок 2.2). Оси 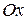, , 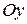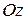называются соответственно осью абсцисс, осью ординат и осью аппликат.

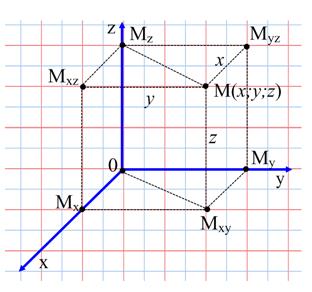
Рисунок 2.2. Прямоугольная система координат в пространстве

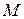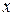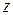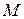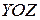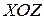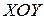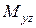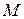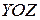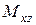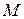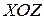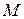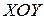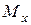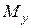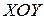Положение любой точки пространства можно охарактеризовать с помощью трёх чисел – абсциссы , ординаты , аппликаты , которые равны расстоянию (взятому с определённым знаком) от точки до координатных плоскостей , , . На рисунке 2.2 проекция точки на плоскость , - проекция точки на плоскость , - проекция точки на плоскость ; и проекции, например, точки в плоскости на координатные ос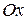и и 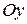, 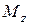- проекция, например, точки 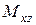в плоскости 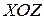на координатную ось 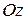. Тогда по определению , , .

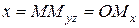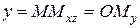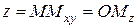Таким образом, с помощью координат мы производим учет всех точек прямой, плоскости или пространства. Такой учет позволяет соединить в единое целое геометрию и алгебру. Каждое понятие, каждая теорема могут быть высказаны как бы на двух языках – на геометрическом и аналитическом, что позволяет переходить от оперирования геометрическим объектом к оперированию его алгебраическим заданием (уравнением, неравенством и т.п.). Решение геометрических задач аналитически (алгебраическим методом) и составляет сущность метода координат.

Рассмотрим основные задачи на прямоугольные координаты на плоскости.