Решение. т.е. ответ совпал с матрицей полученной в предыдущем примере.
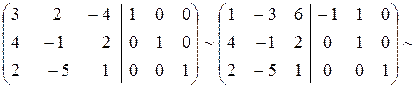
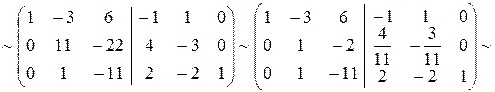
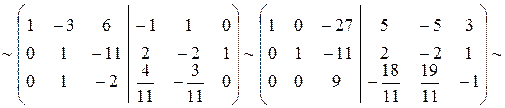
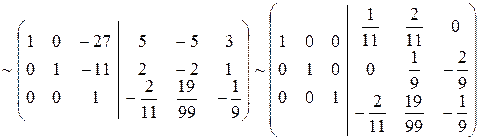 .
.
Таким образом,
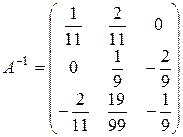 ,
,
т.е. ответ совпал с матрицей полученной в предыдущем примере.
3.6
Пусть дана система 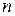 линейных уравнений с
линейных уравнений с 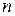 неизвестными (система (3.5)):
неизвестными (система (3.5)):
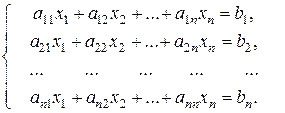
Обозначим 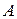 - матрицу из коэффициентов при неизвестных,
- матрицу из коэффициентов при неизвестных, 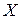 - матрицу-столбец из неизвестных,
- матрицу-столбец из неизвестных, 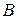 - матрицу-столбец свободных членов, т.е.
- матрицу-столбец свободных членов, т.е.
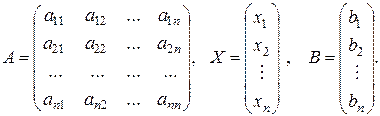
Несложно заметить, что тогда система (3.5) может быть записана в виде матричного уравнения
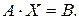 (3.12)
(3.12)
Умножим слева обе части уравнения (3.12) на матрицу, обратную матрице 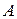 , т.е. на
, т.е. на 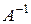 :
:
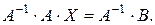 (3.13)
(3.13)
Учитывая, что 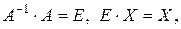 из (3.13) получаем формулу для решения системы в матричной форме :
из (3.13) получаем формулу для решения системы в матричной форме :
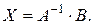 (3.14)
(3.14)
Пример 7. Решить систему из примеров 1 и 4 в матричной форме:
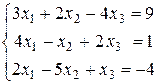 .
.
Решение. Запишем систему в матричной форме:
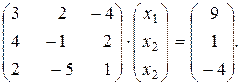
Обозначим 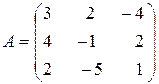 - матрицу из коэффициентов при неизвестных,
- матрицу из коэффициентов при неизвестных, 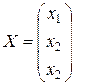 - матрица из неизвестных,
- матрица из неизвестных, 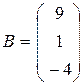 - матрица-столбец свободных членов. Обратная матрица для
- матрица-столбец свободных членов. Обратная матрица для 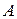 была найдена в примерах 5 и 6:
была найдена в примерах 5 и 6: 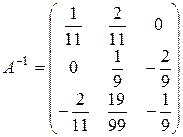 . Тогда находим решение системы:
. Тогда находим решение системы:
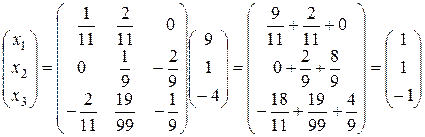 .
.
Таким образом, 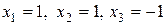 .
.
Замечание. Матричный метод решения систем линейных уравнений применим только тогда, когда число уравнений системы равно числу неизвестных и матрица 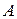 является невырожденной (ограничения те же, что и в методе Крамера).
является невырожденной (ограничения те же, что и в методе Крамера).
3.7
Как было отмечено выше, однородная система линейных уравнений всегда совместна, так как, согласно критерию совместности, ранги основной и расширенной матриц совпадают. Это следует из того, что для однородной системы расширенная матрица содержит столбец нулей – столбец свободных членов.
Для того чтобы однородная система имела единственное решение, необходимо и достаточно, чтобы ранг основной матрицы системы был равен числу неизвестных, т.е. 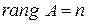 .
.
Единственным решением однородной системы будет нулевое решение. Поэтому для существования ненулевых решений должно выполняться условие 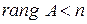 .
.
Если в однородной системе число уравнений равно числу неизвестных, то условие существования ненулевых решений состоит в равенстве нулю основного определителя системы, т.е. 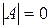 .
.
Лекция 4. Линейный оператор и его матрица. Собственные векторы и собственные значения линейного оператора.
План лекции
4.1. Линейные пространства. Понятие n-мерного вектора.
4.2. Размерность и базис линейного пространства. Координаты вектора линейного пространства.
4.3. Определение линейного оператора, примеры.
4.4. Матрица линейного оператора.
4.5. Собственные векторы и собственные значения линейного оператора, их нахождение.
4.1
Пусть L = {а,в,с,…} – множество элементов произвольной природы и P={a,b,g,…} – числовое поле. Определим операцию над элементами из L, условно называемую сложением, и операцию элементов из L на элементы из P, условно называемую умножением элементов из L на числа из P. Причём "a,bÎL:a+bÎL и "aÎL"aÎP:aaÎL.
Множество L называется линейным пространством над полем P (обозначается L(P)), если операции сложения элементов из L и умножения элементов из L на числа из P удовлетворяют аксиомам:
1o. "a,bÎL:a+b=b+a – сложение коммутативно.
2o. "а,b,cÎL:(a+b)+c = a+(b+c) – сложение ассоциативно.
3o. $qÎL:"aÎL:a+q=q+a=a – существует нейтральный элемент по сложению.
4o. "аÎL$(-a)ÎL:a+(-a)=(-a)+a=q – для любого элемента из L существует противоположный элемент по сложению.
5o. "aÎL^1ÎP:a×1=1×a=a – в поле P существует 1 – нейтральный элемент по умножению.
6o. "a,bÎP^"aÎL:(ab)a=a(ba) – ассоциативность относительного умножения элемента из L на произведение чисел из P.
7o. "a,bÎP^"aÎL:(a+b)×a=aa+ba – дистрибутивность умножения элемента из L относительно суммы чисел из P.
8o. "a,bÎL^"aÎP:a(a+b)=aa+ab – дистрибутивность умножения числа из P относительно суммы элементов из L.
Будем называть элементы из L векторами, поэтому линейное пространство L(P) называют и векторным пространством. Заметим, что рассмотренные ранее пространства V2 и V3 являются линейными. Однако, исходя из введенного определения линейного пространства, понятие вектора можно распространить далее и на не геометрические объекты.
Арифметическим вектором, или n-мерным вектором a будем называть упорядоченную последовательность из n чисел a1,a2,…,an и обозначать a=[a1,a2,…,an], где ai( 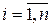 ) – компоненты вектора. Обозначим множество всех n-мерных векторов Tn и введем над ними операции сложения и умножения вектора на число из P по правилам:
) – компоненты вектора. Обозначим множество всех n-мерных векторов Tn и введем над ними операции сложения и умножения вектора на число из P по правилам:
1) "a=[a1,a2,…,an]ÎTn^"b=[b1,b2,…,bn]ÎTn:
a+b=c=[a1+b1,a2+b2,…,an+bn,]ÎTn.
2) "a=[a1,a2,…,an]Î Tn^"lÎP:la=[la1,la2,…,lan]Î Tn.
Можно проверить, что множество Tn удовлетворяет аксиомам 1o - 8o линейного пространства, и поэтому его называют арифметическим n-мерным пространством.
Можно проверить, что множество Tn всех n-мерных векторов a=[a1,a2,…,an] удовлетворяет аксиомам 1o - 8o линейного пространства, и поэтому его называют арифметическим n-мерным пространством.
4.2
Введенные ранее понятия линейно зависимой и линейно независимой систем векторов можно распространить на любую систему векторов, а не только на систему геометрических векторов.
Система векторов a1,a2,…,an линейного пространства L(P) называется линейно зависимой, если их линейная комбинация l1a1+l2a2+…+lnan равна нулю при условии, что не все li равны нулю ( 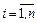 ), и называется линейно независимой, если все li=0 (
), и называется линейно независимой, если все li=0 ( 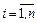 ). Можно дать и другое определение. Система векторов a1,a2,…an – линейно зависимая, если один из векторов может быть выражен через другие, и линейно независимая – в противном случае.
). Можно дать и другое определение. Система векторов a1,a2,…an – линейно зависимая, если один из векторов может быть выражен через другие, и линейно независимая – в противном случае.
Если в линейном пространстве L(P) имеется n линейно независимых векторов, но любые n+1 вектора этого пространства линейно зависимы, то пространство L(P) называют n-мерным, или говорят, что линейное пространство имеет размерность n. Записывают dim L(P)=n.
Таким образом, размерностью линейного пространства называют максимальное число линейно независимых векторов, которые можно выбрать в этом пространстве. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называют бесконечномерным, и пишут dim L(P)=¥.
Максимальное число линейно независимых векторов линейного пространства, через которые можно выразить любой другой вектор этого пространства, называется базисом этого пространства. Таким образом, число векторов базиса показывает, чему равна размерность этого пространства. Каждый вектор линейного пространства может быть единственным образом представлен в виде линейной комбинации векторов базиса. Так, если е1,е2,…,еn – базис линейного пространства, то для любого вектора aÎL(P) разложение a=l1е1+l2е2+…+lnеn единственно. Коэффициенты разложения вектора по векторам базиса линейного пространства называются координатами вектора в данном базисе, т.е. можно записать a=(l1,l2,…,ln)B, где B={е1, е2,,…,еn}.
Базис линейного пространства может быть выбран неоднозначно, но для данного линейного пространства количество векторов в базисе должно быть постоянно. Таким образом, постоянной существенной характеристикой линейного пространства является его размерность.
4.3
Будем говорить, что в линейном пространстве 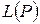 задано преобразование или оператор
задано преобразование или оператор 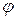 , если каждому вектору
, если каждому вектору 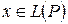 по некоторому правилу поставлен в соответствие вектор
по некоторому правилу поставлен в соответствие вектор 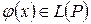 .
.
Оператор 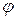 называется линейным, если для любых двух векторов
называется линейным, если для любых двух векторов 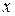 и
и 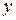 из
из 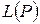 и для любого числа
и для любого числа 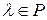 выполняются условия:
выполняются условия:
1. Образ суммы двух векторов равен сумме образов этих векторов, т. е.
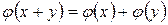 . (4.1)
. (4.1)
2. Образ произведения вектора на число равен произведению этого числа на образ вектора, т.е.
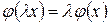 . (4.2)
. (4.2)
Условия (4.1) и (4.2) в определении линейного оператора можно заменить одним условием: образ линейной комбинации векторов линейного пространства равен линейной комбинации образов этих векторов, т.е. для любых двух векторов 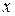 и
и 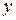 из
из 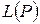 и для любых чисел
и для любых чисел 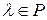 и
и 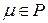 :
:
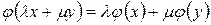 . (4.3)
. (4.3)
Примеры линейных операторов.
1. Линейное преобразование называется тождественным, если оно преобразует любой вектор в самого себя, и обозначается Е. Таким образом,
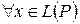 : E(x)=x.
: E(x)=x.
2. Нуль-оператор – это оператор, переводящий любой вектор в нуль-вектор, и обозначается 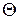 . Таким образом,
. Таким образом,
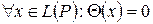 .
.
3. Оператор подобия задаётся правилом:
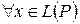 и
и 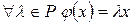 .
.
4.4
Пусть в n-мерном линейном пространстве 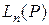 с базисом
с базисом 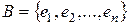 задан линейный оператор
задан линейный оператор 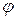 . Образами базисных векторов будут векторы:
. Образами базисных векторов будут векторы: 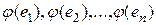 этого же линейного пространства, поэтому каждый из них можно разложить единственным образом по векторам базиса:
этого же линейного пространства, поэтому каждый из них можно разложить единственным образом по векторам базиса:
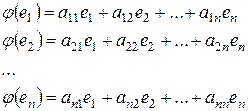 (4.4)
(4.4)
Матрицей линейного оператора 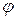 в базисе В называется квадратная матрица
в базисе В называется квадратная матрица 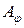 , составленная из коэффициентов разложения образов базисных векторов по векторам базиса, т.е.
, составленная из коэффициентов разложения образов базисных векторов по векторам базиса, т.е.
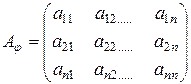 . (4.5)
. (4.5)
Для приведённых в п. 4.3 примеров матрицы линейных операторов имеют вид:
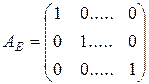 ,
, 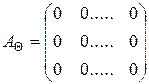 ,
, 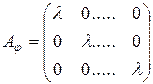 .
.
Отметим тот факт, что матрица линейного оператора зависит от выбора базиса.
Пример 1. Проверить, что заданный в пространстве Т3 оператор 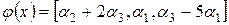
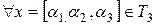 является линейным. Найти матрицу этого оператора в базисе
является линейным. Найти матрицу этого оператора в базисе 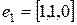 ,
, 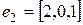 ,
, 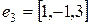 .
.
Решение. Проверим условие (4.3):
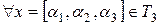 и
и 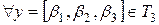 ,
, 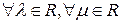 :
: 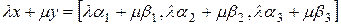 ,
,
тогда
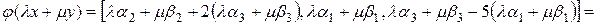
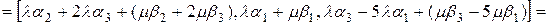
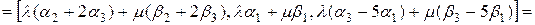
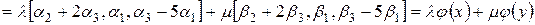 .
.
Следовательно, данный оператор является линейным.
Найдём образы базисных векторов 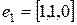 ,
, 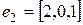 ,
, 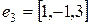 :
:
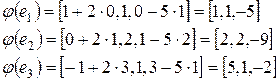 .
.
Разлагаем образы базисных векторов по векторам базиса:
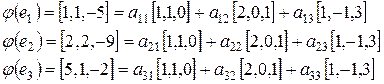
Для определения элементов матрицы линейного оператора получаем системы:
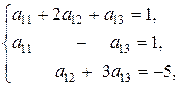
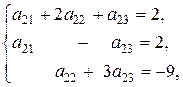
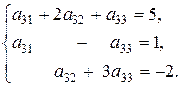
С учетом, что матрица из коэффициентов при неизвестных во всех полученных системах одинаковая, эти системы лучше решать матричным способом.
Запишем системы в матричной форме:
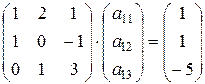 ,
, 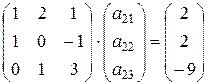 ,
, 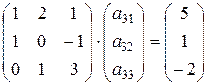
Находим обратную матрицу:
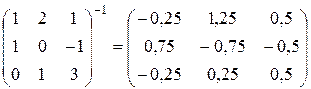 (проверить самостоятельно).
(проверить самостоятельно).
Следовательно, 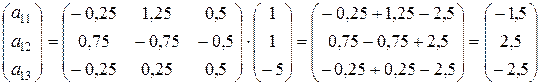 ,
, 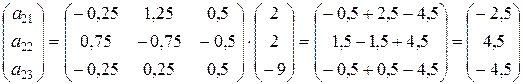 ,
, 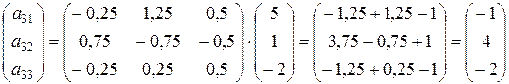 .
.
Таким образом, данный оператор в указанном базисе имеет матрицу:
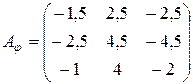 .
.
4.5
Ненулевой вектор 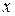 х линейного пространства
х линейного пространства 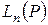 называется собственным вектором линейного оператора, если
называется собственным вектором линейного оператора, если
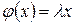 . (4.6)
. (4.6)
В этом случае 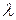 называется собственным значением линейного оператора или характеристическим числом оператора
называется собственным значением линейного оператора или характеристическим числом оператора 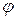 .
.
Перепишем равенство (4.6) в виде
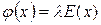 , (4.7)
, (4.7)
где 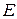 – тождественный оператор, или (4.7) перепишем в виде
– тождественный оператор, или (4.7) перепишем в виде
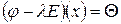 . (4.8)
. (4.8)
Если линейный оператор 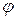 задан матрицей
задан матрицей 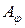 , то координаты образа равны произведению координат прообраза на матрицу линейного оператора
, то координаты образа равны произведению координат прообраза на матрицу линейного оператора 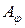 в данном базисе. Поэтому (4.8) можно переписать в виде
в данном базисе. Поэтому (4.8) можно переписать в виде
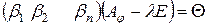 ,(4.9)
,(4.9)
где 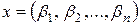 ,
,
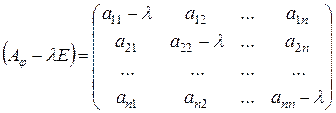 .
.
Из равенства (4.9) получаем однородную систему 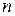 линейных уравнений с n-неизвестными
линейных уравнений с n-неизвестными 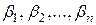 . Эта система всегда имеет нулевое решение, которое, согласно определению, нас не устраивает. Для того чтобы эта система имела ненулевые решения, необходимо и достаточно, чтобы определитель этой системы был равен нулю, т.е.
. Эта система всегда имеет нулевое решение, которое, согласно определению, нас не устраивает. Для того чтобы эта система имела ненулевые решения, необходимо и достаточно, чтобы определитель этой системы был равен нулю, т.е.
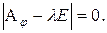 (4.10)
(4.10)
Уравнение (4.10) называется характеристическим уравнением матрицы оператора 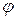 в базисе В. Решая его, находим собственные значения линейного оператора. Подставляя найденные собственные значения в систему (4.9), найдём собственные векторы, принадлежащие собственным значениям линейного оператора.
в базисе В. Решая его, находим собственные значения линейного оператора. Подставляя найденные собственные значения в систему (4.9), найдём собственные векторы, принадлежащие собственным значениям линейного оператора.
Пример 2. Линейный оператор 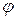 задан матрицей
задан матрицей 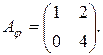
Найти собственные векторы и собственные значения линейного оператора.
Дата добавления: 2015-08-21; просмотров: 1400;
