Решение. 1. Определяем координаты центра тяжести поперечного сечения.
1. Определяем координаты центра тяжести поперечного сечения.
Размеры и геометрические характеристики уголка и швеллера устанавливаем по сортаментам. Вычерчиваем сечение в масштабе (см. рис. 1). Выбираем оси сравненияx и y, располагая их по контуру швеллера. Именно в этих осях мы и будем определять положение центра тяжести всего сечения. Для каждого элемента сечения (уголка, швеллера и полосы) проводим собственные центральные оси 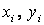 (
( 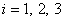 ), параллельные выбранным осям сравнения x и y.
), параллельные выбранным осям сравнения x и y.
Координаты центра тяжести всего поперечного сечения (точка С), состоящего из трех элементов (уголка – 1, швеллера – 2 и полосы – 3), вычисляются по формулам:
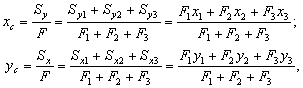
где 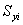 и
и 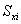 – статические моменты соответствующего элемента относительно осей сравнения;
– статические моменты соответствующего элемента относительно осей сравнения; 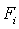 – площадь элемента;
– площадь элемента; 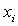 и
и 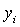 – координаты центра тяжести элемента
– координаты центра тяжести элемента 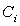 в осях сравнения. Вычисления производим в табличной форме (таблица 1).
в осях сравнения. Вычисления производим в табличной форме (таблица 1).
Таблица 1. Определение координат центра тяжести поперечного сечения
| Номер элемента | Наименование элемента | Площадь элемента
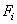 , см2 , см2
| Координаты
центра тяжести элемента 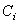
| Статические моменты
элемента относительно осей сравнения 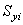 и и 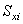
| ||
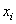 , см , см
| 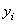 , см , см
| 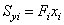 , см3 , см3
| 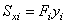 , см3 , см3
| |||
| Уголок | 10,67 | -2,02 | 17,02 | -21,55 | 181,60 | |
| Швеллер | 26,70 | 2,21 | 11,00 | 59,01 | 293,70 | |
| Полоса | 36,00 | 9,00 | -1,00 | 324,00 | -36,00 | |
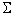
| ВСЕ СЕЧЕНИЕ | 73,37 | 361,46 | 439,30 |
Координаты центра тяжести поперечного сечения (точка С) в осях сравнения x, y:
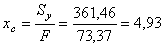 см;
см; 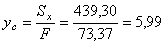 см.
см.
По найденным значениям 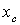 и
и 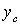 отмечаем на чертеже центр тяжести всего сечения точку С (см. рисунок 1) и проводим центральные оси
отмечаем на чертеже центр тяжести всего сечения точку С (см. рисунок 1) и проводим центральные оси 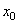 и
и 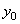 .
.
Заметим, что центр тяжести всей фигуры должен располагаться внутри треугольника, вершинами которого являются центры тяжести элементов поперечного сечения.
2. Вычисляем моменты инерции всего поперечного сечения относительно центральных осей 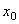 и
и 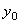 .
.
Осевые и центробежный моменты инерции сечения относительно центральных осей определяются по следующим формулам:
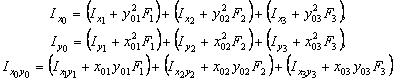
Значения осевых моментов инерции уголка 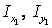 и швеллера
и швеллера 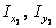 относительно собственных центральных осей
относительно собственных центральных осей 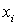 и
и 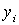 определяем по сортаменту. Для полосы осевые моменты инерции соответственно равны:
определяем по сортаменту. Для полосы осевые моменты инерции соответственно равны:
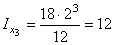 см4;
см4; 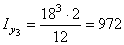 см4.
см4.
Центробежные моменты инерции швеллера  и полосы
и полосы 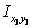 равны нулю, поскольку их собственные центральные оси являются осями симметрии.
равны нулю, поскольку их собственные центральные оси являются осями симметрии.
Центробежный момент инерции уголка 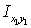 относительно собственных центральных осей
относительно собственных центральных осей 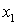 и
и 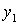 вычисляется по формуле
вычисляется по формуле
 ,
,
где  и
и 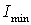 – максимальный и минимальный главные моменты инерции уголка соответственно. По сортаменту (см. прил. 1) находим, что
– максимальный и минимальный главные моменты инерции уголка соответственно. По сортаменту (см. прил. 1) находим, что 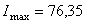 см4, а
см4, а 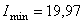 см4.
см4.
Центробежный момент инерции уголка не равен нулю, поскольку оси 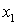 и
и 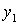 не являются для него главными центральными осями инерции (главные центральные оси для равнобокого уголка повернуты относительно осей
не являются для него главными центральными осями инерции (главные центральные оси для равнобокого уголка повернуты относительно осей 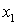 и
и 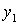 на угол 450).
на угол 450).
Знак центробежного момента инерции уголка (как, впрочем, и для любой другой фигуры) зависит от направления координатных осей. Он легко определяется следующим образом. Согласно определению, центробежный момент инерции фигуры равен интегралу, в котором элементарная площадка 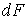 умножается на произведение расстояний от этой площадки до координатных осей. Мысленно разделим уголок на три площади, расположенные, в нашем случае, в первом, третьем и четвертом квадрантах. Эти площади, в свою очередь, разобьем на элементарные площадки. Видно, что для элементарных площадок, расположенных в первом и третьем квадрантах, расстояния от элементарных площадок до координатных осей имеют одинаковый знак. Поэтому при интегрировании по площади, расположенной в этих квадрантах, мы получим знак «плюс». В четвертом квадранте расстояния от площадок до координатных осей имеют разные знаки, что при интегрировании даст знак «минус». Очевидно, что, суммируя полученные результаты, мы, в итоге, получим положительное значение центробежного момента инерции уголка. Следовательно,
умножается на произведение расстояний от этой площадки до координатных осей. Мысленно разделим уголок на три площади, расположенные, в нашем случае, в первом, третьем и четвертом квадрантах. Эти площади, в свою очередь, разобьем на элементарные площадки. Видно, что для элементарных площадок, расположенных в первом и третьем квадрантах, расстояния от элементарных площадок до координатных осей имеют одинаковый знак. Поэтому при интегрировании по площади, расположенной в этих квадрантах, мы получим знак «плюс». В четвертом квадранте расстояния от площадок до координатных осей имеют разные знаки, что при интегрировании даст знак «минус». Очевидно, что, суммируя полученные результаты, мы, в итоге, получим положительное значение центробежного момента инерции уголка. Следовательно,
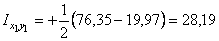 см4.
см4.
Теперь определяем координаты центров тяжести отдельных элементов Ci в центральных осях 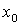 и
и 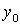 :
:
для уголка
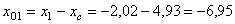 см;
см;
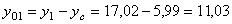 см;
см;
для швеллера
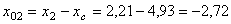 см;
см;
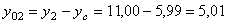 см;
см;
для полосы
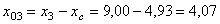 см;
см;
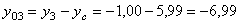 см.
см.
Дальнейшие вычисления моментов инерции всего поперечного сечения относительно центральных осей 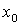 и
и 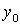 производим в табличной форме (таблица 2).
производим в табличной форме (таблица 2).
Таблица 2. Определение моментов инерции сечения относительно центральных осей 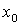 и
и 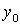
| Номер элемента | Наименование элемента | Площадь
элемента 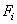 , см2 , см2
| Моменты инерции относительно
собственных центральных осей 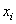 и и 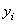
| Координаты центра
тяжести в осях 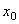 и и 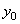
| |||
 , см4 , см4
| 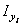 , см4 , см4
| 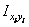 , см4 , см4
| 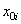 , см , см
|  , см , см
| |||
| Уголок | 10,67 | 48,16 | 48,16 | 28,19 | -6,95 | 11,03 | |
| Швеллер | 26,70 | 2110,00 | 151,00 | -2,72 | 5,01 | ||
| Полоса | 36,00 | 12,00 | 972,00 | 4,07 | -6,99 | ||
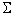
| ВСЕ СЕЧЕНИЕ | 73,37 |
Продолжение таблицы 2
| Наименование элемента | "Переносные" моменты инерции, см4 | Моменты инерции относительно
центральных осей 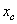 и и 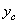 , см4 , см4
| ||||
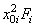
| 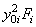
| 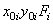
| 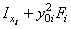
| 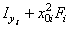
| 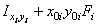
| |
| Уголок | 515,39 | 1298,12 | -817,95 | 1346,28 | 563,55 | -789,76 |
| Швеллер | 197,54 | 670,17 | -363,85 | 2780,17 | 348,54 | -363,85 |
| Полоса | 596,34 | 1758,96 | -1024,17 | 1770,96 | 1568,34 | -1024,17 |
| ВСЕ СЕЧЕНИЕ | 5897,41 | 2480,43 | -2177,78 |
После округления вычисленных значений моментов инерции до трех значащих цифр, окончательно, получим
 см4;
см4; 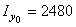 см4;
см4; 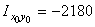 см4.
см4.
3. Определяем положение главных центральных осей инерции u и v.
Угол наклона главных центральных осей u и v к центральным осям 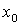 и
и 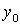 соответственно определяем из следующей формулы:
соответственно определяем из следующей формулы:
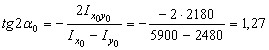 .
.
Отсюда находим, что 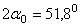 и
и 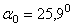 .
.
Откладываем положительное значение угла 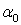 от оси
от оси 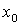 против хода часовой стрелки и проводим главные центральные оси u и v (см. рисунок 1).
против хода часовой стрелки и проводим главные центральные оси u и v (см. рисунок 1).
Ось, относительно которой момент инерции максимален, составляет меньший угол с той из центральных осей 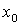 или
или 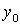 , относительно которой осевой момент больше. Поскольку
, относительно которой осевой момент больше. Поскольку  см4 больше, чем
см4 больше, чем 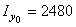 см4, ось u является осьюотносительно которой момент инерции сечения максимален, то есть ось u – ось max. Соответственно, ось v является осью min.
см4, ось u является осьюотносительно которой момент инерции сечения максимален, то есть ось u – ось max. Соответственно, ось v является осью min.
4. Вычисляем значения главных центральных моментов инерции 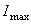 и
и 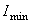 для заданного поперечного сечения.
для заданного поперечного сечения.
Значения главных центральных моментов инерции всей фигуры определяются по формуле
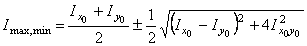 .
.
Тогда
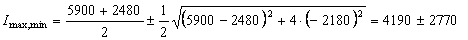 см4;
см4;
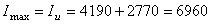 см4;
см4; 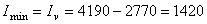 см4.
см4.
Контролем правильности последних вычисленийможет служитьследующее условие:
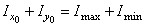 .
.
Имеем
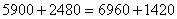 ,
, 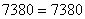 .
.
Дата добавления: 2015-08-08; просмотров: 3781;
